
Ce cours de logique et raisonnement est conforme au programme des classes préparatoires scientifiques des filières MPSI, PCSI, MP2I et PTSI. Dans ce cours, vous apprendrez à raisonner de manière rigoureuse et cohérente et à formuler des arguments clairs et à les présenter de manière logique et structurée. Vous apprendrez également les différentes techniques de démonstration, telles que le raisonnement directe, le raisonnement par contraposée, le raisonnement par équivalence, le raisonnement par l’absurde, le raisonnement par disjonction des cas, le raisonnement par analyse-synthèse et le raisonnement par récurrence.
Pour consolider vos connaissances et devenir plus à l’aise avec les concepts abordés dans ce cours, n’hésitez pas à consulter notre série d’exercices corrigés en logique et raisonnement.
- I) Logique
- II) Raisonnement
I) Logique
Définition 1 (proposition ou assertion) :
Une proposition (on dit aussi assertion) est une phrase à laquelle on peut attribuer une et une seule des deux valeurs logique vraie ou fausse.
Exemple d’une proposition :
«1 \leq 2 » est une assertion vraie.
« i \in \mathbb{R} » est une assertion fausse.
Définition 2 (fonction propositionnelle) :
Une fonction propositionnelle est une expression contenant une ou plusieurs variables libre et qui est susceptible de devenir une proposition vraie ou fausse si l’on attribue à ces variables certaines valeurs particulières ou si on lie ces variables par des quantificateurs.
Exemple d’une fonction propositionnelle :
On peut définir sur \mathbb{R} ou sur \mathbb{C} la fonction propositionnelle P(x) : «x^{2}-x-2=0 ».
P(0) est une proposition fausse.
P(2) est une proposition vraie.
Définition 3 (quantificateur universel, quantificateur existentiel) :
Soit P(x) une fonction propositionnelle sur un ensemble E.
i) « \forall x \in E, P(x) » est une proposition qui signifie que pour tout élément x fixé dans \mathrm{E}, la proposition P(x) est vraie.
Le quantificateur universel se note « \forall » et se lit « pour tout » ou « quel que soit».
ii) « \exists x \in E, P(x) » est une proposition qui signifie qu’il existe au moins un élément x appartenant à E, tel que la proposition P(x) est vraie.
Le quantificateur existentiel se note « \exists » et se lit « il existe ».
iii) Pour exprimer l’existence et l’unicité on utilise le symbole « \exists! » qui se lit « il existe un unique » ou « il existe un et un seul ».
Exemples d’utilisation des quantificateurs :
i) « \forall x \in \mathbb{R}, \exists y \in \mathbb{R}, \quad x \leq y » est une proposition vraie.
ii) « \exists y \in \mathbb{R}, \forall x \in \mathbb{R}, \quad x \leq y » est une proposition fausse.
On remarque d’après ces deux exemples que l’ordre des quantificateurs est important.
iii) « \forall x \in \mathbb{R}, \exists ! y \in \mathbb{R}, \quad x \leq y » est une proposition fausse.
Table de vérité des connecteurs logiques usuels :
On considère deux assertions P et Q. On a la table de vérité suivante :
| P | V | V | F | F | |
| Q | V | F | V | F | |
| Négation | \bar{P} | F | F | V | V |
| Conjonction « et » | P et Q | V | F | F | F |
| Disjonction « ou » | P ou Q | V | V | V | F |
| Implication « \bar{P} ou Q » | P \Rightarrow Q | V | F | V | V |
| Équivalence « ( P \Rightarrow Q ) et ( Q \Rightarrow P ) » | P \Leftrightarrow Q | V | F | F | V |
Exemples d’utilisation des Connecteurs logiques :
i) « \overline{0=1} » est une assertion vraie.
ii) « 1 \leq 2 et 2 \leq 1 » est une assertion fausse.
iii) « 1 \leq 2 ou 2 \leq 1 » est une assertion vraie.
iv) « \overline{0=1} \Rightarrow \sqrt{2} \in \mathbb{Q} » est une assertion fausse.
v) « 4 est un carré parfait \Leftrightarrow-1 est un entier naturel » est une assertion fausse.
Quand est-ce que deux propositions sont équivalentes ?
On dit que deux propositions P et Q sont équivalentes lorsqu’elles ont la même valeur de vérité.
Propriétés des connecteurs logiques «et» et «ou» :
| Propriété | Proposition | Son équivalent |
| Commutativité de « et » | « P et Q » | « Q et P » |
| Commutativité de « ou » | « P ou Q » | « Q ou P » |
| Associativité de « et » | « P et (Q et R) » | « (P et Q) et R) » |
| Associativité de « ou » | « P ou (Q ou R) » | « (P ou Q) ou R) » |
| « et » est distributive par rapport à « ou » | « P et (Q ou R) » | « (P et Q) ou (P et R) » |
| « ou » est distributive par rapport à « et » | « P ou (Q et R) » | « (P ou Q) et (P ou R) » |
Remarque 1 : Pour bien appliquer la distributivité rappelez-vous que la multiplication est distributive par rapport à l’addition mais l’addition n’est pas distributive par rapport à la multiplication.
Lois de Morgan :
| Proposition | Sa négation |
| P | « \bar{P}» ; « non P» |
| « P et Q» | « \bar{P} ou \bar{Q}» |
| « P ou Q» | « \bar{P} et \bar{Q}» |
Comment formuler la négation d’une proposition ?
| Opérateur | Sa négation |
| \forall | \exists |
| et | ou |
| \leq | > |
| < | \geq |
| \in | \notin |
| \subset | \not\subset |
| = | \ne |
Remarque 2 : Lorsque l’un des opérateurs « \leq », « > », « < », « \geq », « \in », « \notin », « \subset », «\not\subset », « = », « \ne » vient directement après l’un des quantificateurs \forall ou \exists, on ne le modifie pas lorsqu’on applique la négation.
Exemples de négation de propositions :
| Proposition | Sa négation |
| \exists x \in \mathbb{R},\quad x>0 | \forall x \in \mathbb{R}, \quad x \leq 0 |
| \forall n \in \mathbb{N}, \quad ( n=1 \text { ou } n \in \mathbb{Z}) | \exists n \in \mathbb{N},\quad ( n \neq 1 \text { et } n \notin \mathbb{Z}) |
| \forall\varepsilon>0, \exists x \in] 0,+\infty[, \quad x+1>\varepsilon | \exists\varepsilon>0, \forall x \in] 0,+\infty[, \quad x+1 \leq \varepsilon |
| \forall x>0, \quad x \in \mathbb{Z} \Rightarrow x \in \mathbb{N} | \exists x>0, \quad x \in \mathbb{Z} \text { et } x \notin \mathbb{N} |
II) Raisonnement
1) Comment prouver une implication « P\Rightarrow Q » ?
Méthode 1 : Raisonnement directe (ou par déductions successives)
On suppose que P est vraie et par des déductions successives, on démontre que Q est vraie.
Méthode 2 : Raisonnement par contraposition
Pour montrer une implication « \mathrm{P} \Rightarrow Q » il suffit de montrer sa contraposée « \bar{Q} \Rightarrow \bar{P} ».
2) Condition nécessaire, condition suffisante
Soit P et Q deux propositions. Si l’implication « P\Rightarrow Q » est vraie, on dit que :
Q est une condition nécessaire pour P. Autrement dit si P est vraie alors nécessairement Q est vraie.
P est une condition suffisante pour Q. Autrement dit pour que Q soit vraie, il suffit que P soit vraie.
Exemples de conditions nécessaires et de conditions suffisantes :
On a l’implication \forall n \in \mathbb{Z},\quad n impair \Rightarrow 8 \mid n^{2}-1.
La proposition « 8 \mid n^{2}-1 » est une condition nécessaire pour la proposition « \mathrm{n} impair».
La proposition « n impair» est une condition suffisante pour la proposition «8| n^{2}-1 ».
Remarque 3 : Dire que Q est une condition nécessaire et suffisante pour P signifie que «P \LeftrightarrowQ ».
3) Comment montrer une équivalence « P \Leftrightarrow Q » ?
Méthode 1 : Raisonnement par implication et implication réciproque
Pour montrer que « P \Leftrightarrow Q », on montre d’abord l’implication directe « P \Rightarrow Q » puis on montre l’implication réciproque « Q \Rightarrow P ».
Méthode 2 : raisonnement par équivalences successives
Pour montrer que « \mathrm{P} \Leftrightarrow \mathrm{Q} » on procède par une suite d’équivalences successives reliant \mathrm{P} et \mathrm{Q}, comme suit :
« \mathrm{P} \Leftrightarrow Q_{1} »
« Q_{1} \Leftrightarrow Q_{2} »
………………………
« Q_{n-1} \Leftrightarrow Q_{n} »
« Q_{n} \Leftrightarrow Q »
Méthode 3 : Utiliser l’équivalence entre « P \Leftrightarrow Q » et « \bar{P} \Leftrightarrow \bar{Q} »
Pour montrer que « P \Leftrightarrow Q » il est parfois plus facile de montrer d’abord que « \bar{P} \Leftrightarrow \bar{Q} »
4) Raisonnement par l’absurde
Pour montrer qu’une proposition P est vraie, on suppose que la proposition \bar{P} est vraie et on cherche une contradiction.
5) Raisonnement par disjonction des cas
On va présenter le principe du raisonnement par disjonction en traitant des exemples.
6) Raisonnement par analyse-synthèse
On utilise souvent le raisonnement par analyse-synthèse lorsqu’on cherche l’ensemble des solutions d’un problème donné.
Un raisonnement par analyse-synthèse se déroule en deux étapes :
- Étape de l’analyse :
On suppose que le problème en question admet une solution, puis par des déductions successives on trouve des conditions nécessaires que doit vérifier cette solution. - Étape de la synthèse :
On examine tous les objets vérifiant les conditions nécessaires accumulées (ce sont les seuls candidats pouvant être des solutions) et on détermine parmi eux lesquels sont réellement des solutions.
7) Raisonnement par récurrence
a) Récurrence simple
Pour montrer par récurrence simple qu’une propriété \mathcal{P}(n) est vraie pour tout entier naturel n tel que n \geq n_{0}, on suite les trois étapes suivantes :
- Étape 1 : Initialisation
On vérifie que \mathcal{P}\left(n_{0}\right) est vraie. - Étape 2 : Hérédité
On fixe un entier naturel n tel que n \geq n_{0}. On suppose que \mathcal{P}(n) est vraie et on montre que \mathcal{P}(n+1) est vraie. - Étape 3 : Conclusion
\forall n \geq n_{0}, \mathcal{P}(n)
b) Récurrence à pas multiples
Soit k \in \mathbb{N}^{*}, pour montrer par récurrence à k-pas qu’une propriété \mathcal{P}(n) est vraie pour tout entier naturel n tel que n \geq n_{0}, on suite les trois étapes suivantes :
- Étape 1 : Initialisation
On vérifie que \mathcal{P}\left(n_{0}\right), \mathcal{P}\left(n_{0}+1\right), \ldots, \mathcal{P}\left(n_{0}+k-1\right) sont vraies. - Étape 2 : Hérédité
On fixe un entier naturel n tel que n \geq n_{0}. On suppose que \mathcal{P}(n), \mathcal{P}(n+1), \ldots, \mathcal{P}(n+k-1) sont vraies et on montre que \mathcal{P}(n+k) est vraie. - Étape 3 : Conclusion
\forall n \geq n_{0}, \mathcal{P}(n)
c) Récurrence forte
Pour montrer par récurrence forte qu’une propriété \mathcal{P}(n) est vraie pour tout entier naturel n tel que n \geq n_{0}, on suite les trois étapes suivantes :
- Étape 1 : Initialisation
On vérifie que \mathcal{P}\left(n_{0}\right) est vraie - Étape 2 : Hérédité
On fixe un entier naturel n tel que n \geq n_{0}. On suppose que \forall k \in \llbracket n_{0}, n \rrbracket, \mathcal{P}(k) est vraie et on montre que \mathcal{P}(n+1) est vraie. - Étape 3 : Conclusion
\forall n \geq n_{0}, \mathcal{P}(n)

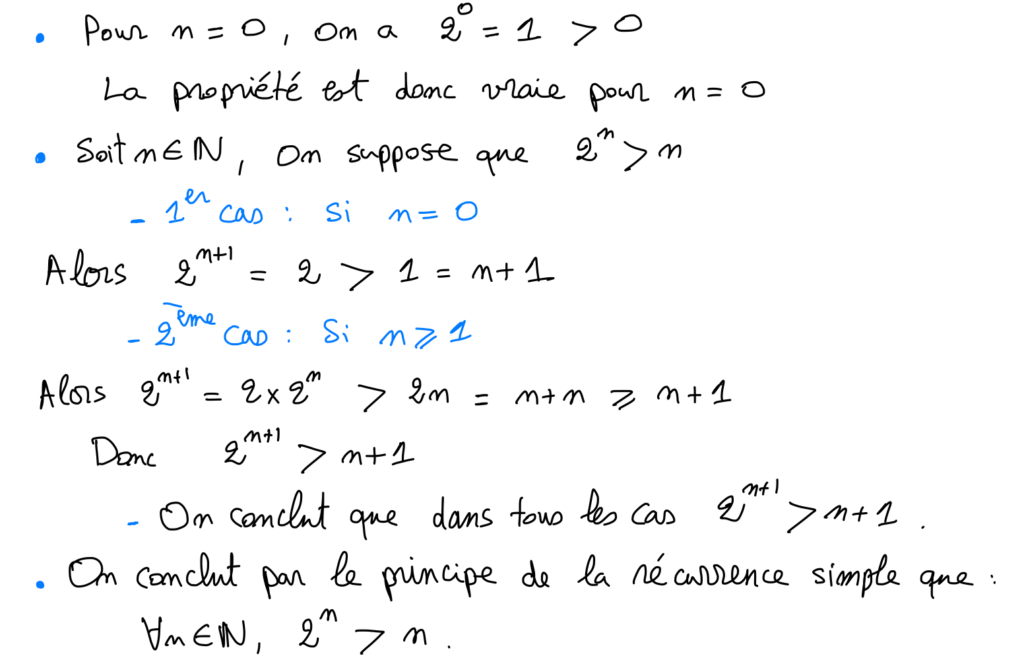
Une réponse