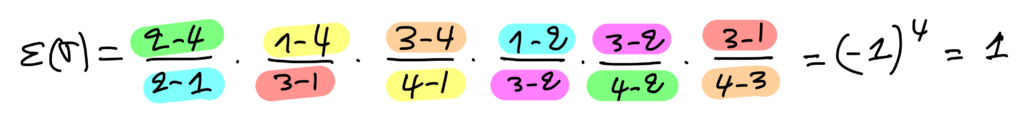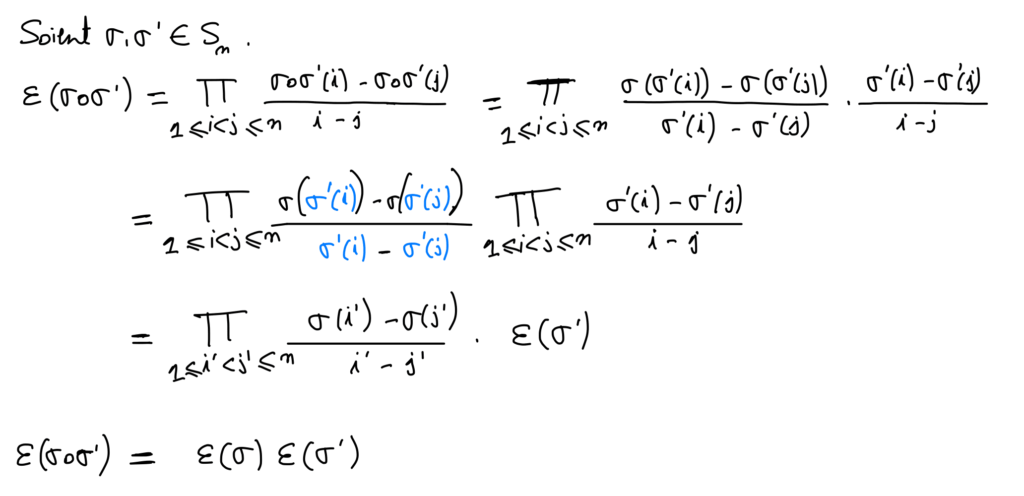Ce cours sur le groupe symétrique est introduit dans le programme des filières MPSI et MP2I en vue de l’étude des déterminants, mais aussi pour son intérêt propre et ses interventions possibles dans diverses questions d’algèbre et de probabilités
I) Premières notions sur le groupe symétrique
Soit A un ensemble non vide.
i) On appelle permutation de A toute application bijective de A dans A.
ii) On note S(A) l’ensemble des permutations de A.
iii) (S(A), \circ ) est un groupe.
iv) On note S_{n}=S(\llbracket 1,n \rrbracket ) . ( S_{n} , \circ ) est un groupe appelé groupe symétrique d’indice n.
v) Si \sigma \in S_{n} , on note \sigma = \begin{pmatrix} 1&2& \dots &n \\ \sigma (1)& \sigma (2)&\dots & \sigma (n) \end{pmatrix} .
vi) card(S_{n})=n!
Exemple 1 :
1) S_{2}= \{ id_{ \{1 ; \ 2 \}} \ ; \ \tau_{1,2}=\begin{pmatrix} 1&2 \\ 2&1 \end{pmatrix} \}
2) S_{3}= \{ id_{ \llbracket1 , 3 \rrbracket } \ ; \ \tau_{1,2}=\begin{pmatrix} 1&2 &3\\ 2&1&3 \end{pmatrix} \ ;\tau_{1,3}=\begin{pmatrix} 1&2 &3\\ 3&2&1 \end{pmatrix} \ ; \tau_{2,3}=\begin{pmatrix} 1&2 &3\\ 1&3&2 \end{pmatrix} \ ; \begin{pmatrix} 1&2 &3\\ 2&3&1 \end{pmatrix} \ ; \begin{pmatrix} 1&2 &3\\ 3&1&2 \end{pmatrix} \}
3) La permutation \sigma = \begin{pmatrix} 1&2&3&4 \\ 2&1&4&3 \end{pmatrix} est définie par \sigma(1)=2 , \ \sigma(2)=1, \ \sigma(3)=4, \ \sigma(4)=3.
II) Les transpositions
Définition d’une transposition :
Soient i,j\in \llbracket1,n \rrbracket tels que i \ne j
On appelle transposition sur i,j la permutation de S_{n} notée \tau_{i,j} , définie par : \forall k\in \llbracket 1,n \rrbracket \setminus \{i,j \} \ \sigma(k)=k , \ \sigma(i)=j \ et \ \sigma(j)=i.
Exemple 2 :
1) Dans S_{4} on a : \tau_{1,2}=\begin{pmatrix} 1&2&3&4\\ 2&1&3&4 \end{pmatrix} \ et \ \tau_{2,4}=\begin{pmatrix} 1&2&3&4\\ 1&4&3&2 \end{pmatrix}
2) Dans S_{3} on a : \tau_{1,2}=\begin{pmatrix} 1&2&3\\ 2&1&3 \end{pmatrix} \ et \ \tau_{2,3}=\begin{pmatrix} 1&2&3\\ 1&3&2 \end{pmatrix}
Remarque 1 : Pour tout i,j \in \llbracket 1,n \rrbracket tels que i \ne j on a :
i) \ \tau_{i,j}=\tau_{j,i}
ii) \ \tau_{i,j}^{2}=id donc \tau_{i,j} est inversible et \tau_{i,j}^{-1}=\tau_{i,j}
Proposition 1 :
Toute permutation se décompose en produit de transpositions.
Remarque 2 : La décomposition n’est pas unique mais la parité du nombre de transposition l’est.
III) Les cycles
Définition d’une Orbite
Soient \sigma \in S_{n} , \ i \in \llbracket 1,n \rrbracket .
On appelle orbite de i sous \sigma l’ensemble O_{\sigma}(i)= \{ \sigma^{k}(i) / k\in \mathbb{Z} \}
Exemple 4 :
On pose \sigma=\begin{pmatrix} 1&2&3&4&5&6\\ 2&1&4&5&3&6 \end{pmatrix}
O_{\sigma } (1)= \{ 1 \ ; \ 2 \}=O_{\sigma } (2) , \ O_{\sigma } (3) = O_{\sigma } (4) = O_{\sigma } (5) = \{3 \; \ 4 ; \ 5\}, \ O_{\sigma }(6)=\{ 6 \}
Définition d’un cycle
Soit \sigma \in S_{n} .
i) On dit que \sigma est un cycle lorsque parmi tous les orbites sous \sigma , il n’existe qu’une seule orbite O_{ \sigma } (i), \ i\in \llbracket 1,n \rrbracket non réduite à un élément. Dans ce cas :
– L’orbite O_{ \sigma } (i) est appelée support du cycle \sigma .
– O_{ \sigma } (i) est appelé longueur du cycle.
– On note \sigma = ( i, \ \sigma (i),\ \dots, \ \sigma^{p-1} (i) )
Exemple 5 :
i) Une transposition est un cycle de longueur 2. \tau_{i,j}=(i,j)
ii) \sigma=\begin{pmatrix} 1&2&3&4&5\\ 3&2&5&4&1 \end{pmatrix} \in S_{5} est un cycle de longueur 3. On peut l’écrire \sigma = (1, \ 3, \ 5) .
iii) Si \sigma = (1, \ 3, \ 4, \ 5) \in S_{7} , alors \sigma=\begin{pmatrix} 1&2&3&4&5&6&7\\ 3&2&4&5&1&6&7 \end{pmatrix}
Remarque 3 :
i) Si \sigma = (a_{1}, \ a_{2}, \ \dots , a_{p} ) \in S_{n}, \ alors \ \forall k \in \llbracket 1,p \rrbracket , \ a_{k} = \sigma^{k-1}(a_{1})
ii) \sigma^{p}=id
iii) Deux cycles à supports disjoints commutent. Par exemple, dans S_4 , \ \tau_{1,2} \tau_{3,4}=\tau_{3,4} \tau_{1,2}.
iv) Par contre, si les supports ne sont pas disjoints, il n’ y a pas de commutativité en général. Par exemple, dans S_{3}, \ \tau_{1,2} \tau_{1,3}=\begin{pmatrix}1&2&3 \\ 3&1&2 \end{pmatrix} \ et \ \tau_{1,3} \tau_{1,2}=\begin{pmatrix}1&2&3 \\ 2&3&1 \end{pmatrix} \ donc \ \tau_{1,3} \tau_{1,2} \ne \tau_{1,2} \tau_{1,3}
Proposition 2 :
Toute permutation distincte de l’identité se décompose de manière unique, à l’ordre près des facteurs, en produit de cycles à supports deux à deux disjoints.
Exemple 6 :
i) La permutation \sigma = \begin{pmatrix}1&2&3&4&5&6&7&8&9&10 \\ 3&4&2&1&5&8&6&7&10&9 \end{pmatrix} \in S_{10} se décompose en produit de trois cycles sous la forme \sigma = (1, \ 3, \ 2, \ 4) (6, \ 8, \ 7)(9, \ 10)
ii) On pose \sigma = \begin{pmatrix}1&2&3&4&5&6&7&8 \\ 8&1&3&5&7&6&4&2 \end{pmatrix} \in S_{8} . Calculons \sigma^{100} .
La permutation \sigma se décompose en produit de deux cycles sous la forme \sigma = (1, \ 8, \ 2) (4, \ 5, \ 7) .
Donc \sigma^{100}= ( (1, \ 8, \ 2) (4, \ 5, \ 7) )^{99} \times \sigma
Donc \sigma^{100}= ((1, \ 8, \ 2)^{3} (4, \ 5, \ 7)^{3} )^{33} \times \sigma = id \times \sigma = \sigma
IV) Signature d’une permutation
Définition de la Signature d’une permutation :
Soit \sigma \in S_{n} . On appelle signature de \sigma le produit \varepsilon ( \sigma )= \prod_{1 \leq i<j \leq n} \frac{ \sigma (j)- \sigma(i)} {j-i}
Remarque 4 : Soit \sigma une permutation.
i) \varepsilon (\sigma) \in \{-1 ; \ 1 \}
ii) Si \varepsilon (\sigma) =-1 alors on dit que \sigma est une permutation impaire, sinon on dit que \sigma est une permutation paire.
iii) La signature d’une transposition est -1.
Remarque 5 :
Ceci montre que dans la décomposition d’une permutation en produit de transposition, la parité du nombre de transposition est conservée.
Exemple 8 :
1) \sigma \begin{pmatrix}1&2&3&4 \\ 4&2&1&3 \end{pmatrix} .
On a \sigma = (1, \ 4 , \ 3) est un cycle de longueur 3, donc \varepsilon ( \sigma )= (-1)^{2}=1
2) \sigma \begin{pmatrix}1&2&3&4&5&6&7&8 \\ 2&5&3&6&1&4&8&7 \end{pmatrix} .
\sigma = (1, \ 2, \ 5)(4,\ 6)(7,\ 8) .
\varepsilon ( \sigma )= \varepsilon ( (1, \ 2, \ 5) )\varepsilon ( (4,\ 6) )\varepsilon ( (7,\ 8) )(-1)^{2} (-1)^{1} (-1)^{1}=1