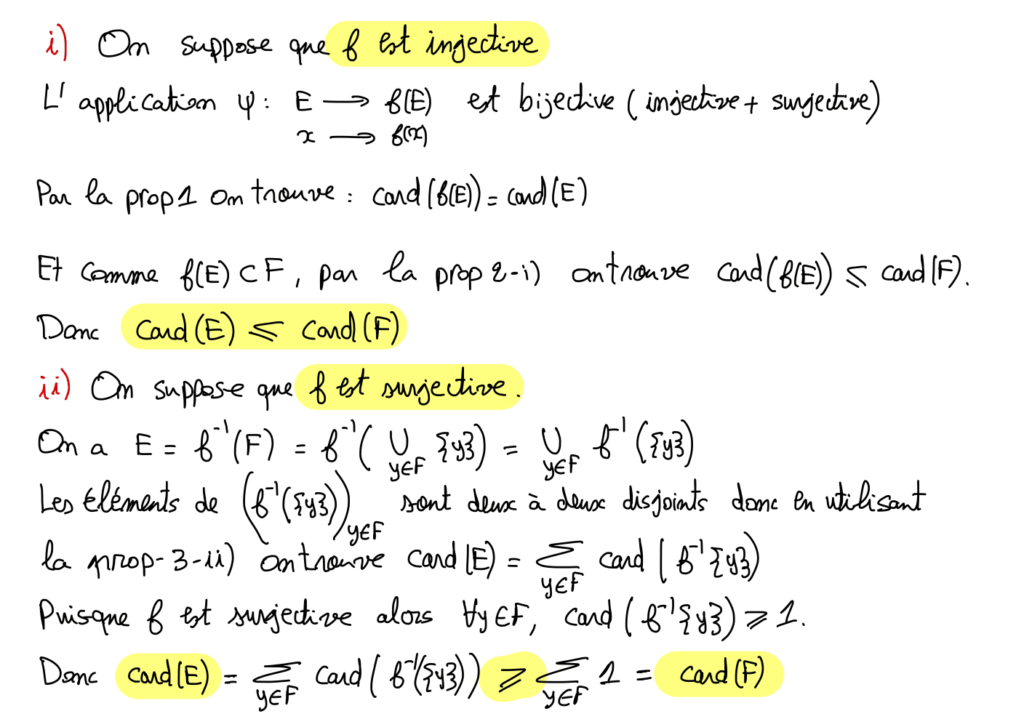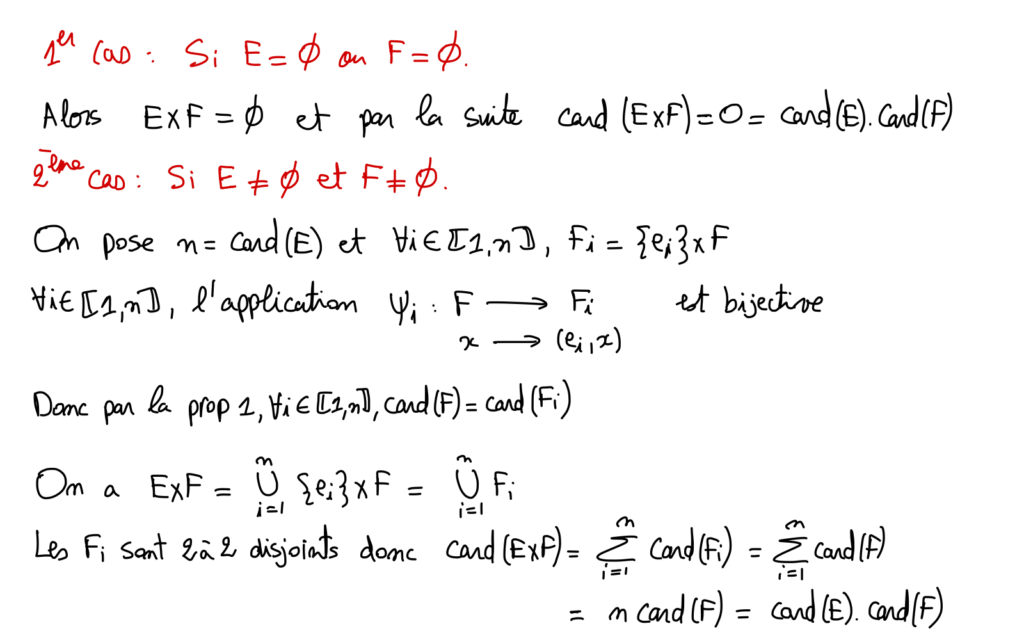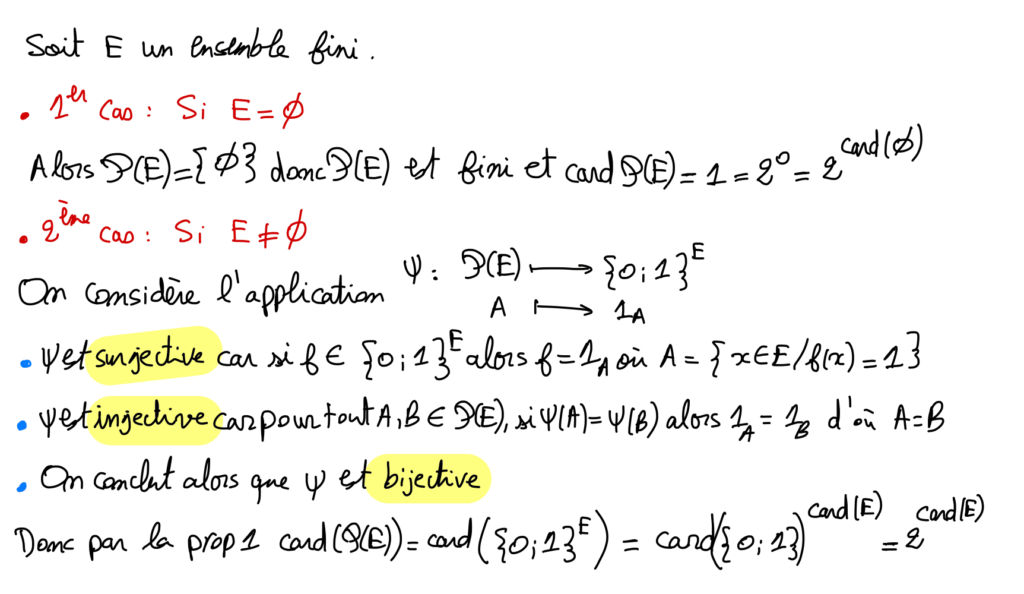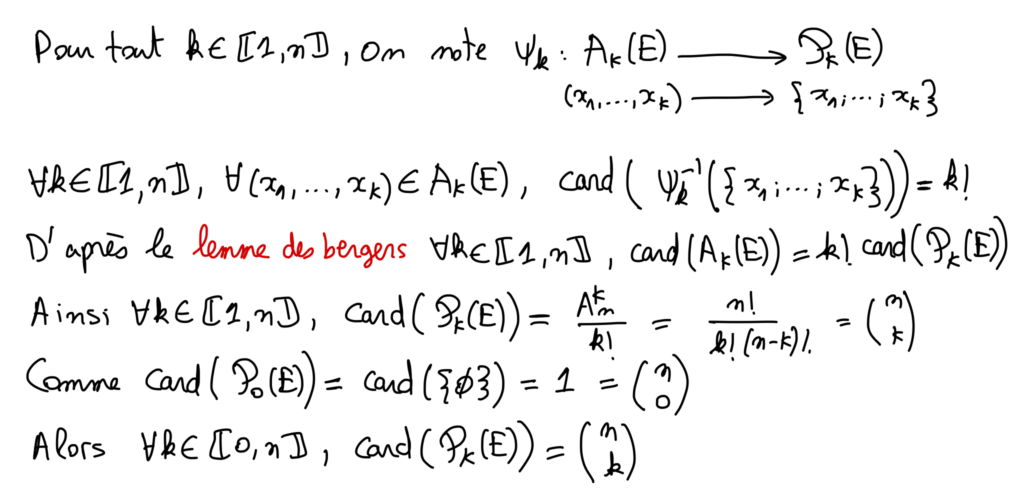Ce cours sur le dénombrement s’adresse aux étudiants des filières MPSI et MP2I. Il est introduit au programme essentiellement en vue de son utilisation en probabilités. Je vous encourage également à consulter notre série d’exercices corrigés sur le dénombrement afin d’assimiler pleinement le contenu du cours.

I) Cardinal d’un ensemble fini

Programme officiel dénombrement MPSI-MP2I partie 1

Proposition-définition 1 : Soit E un ensemble.
On dit que E est un ensemble fini lorsqu’il est vide ou lorsqu’il existe un entier naturel non nul n de façon que E soit en bijection avec \llbracket 1, n \rrbracket .
Dans ce cas, n est unique, on l’appelle cardinal de E et on le note card(E) ou |E|.
On convient que card(\emptyset)=0.
Lorsque E n’est pas fini, on dit que E est infini.

Proposition 1 :
Soit E un ensemble fini. Si F est un ensemble en bijection avec E alors F est fini et \operatorname{card}(F)=\operatorname{card}(E)

Démonstration :

Proposition 2 :
Soit E un ensemble fini.
i) Toute partie F de E est finie et de plus \operatorname{card}(F) \leqslant \operatorname{card}(E).
ii) \forall F \in \mathcal{P}(E), \operatorname{card}(E)=\operatorname{card}(F) \Leftrightarrow E=F.

Remarque 1 :
Soient E un ensemble fini et F un ensemble.
Pour montrer que F=E il suffit de montrer que F \subset E et \operatorname{card}(F)=\operatorname{card}(E).

Proposition 3 :
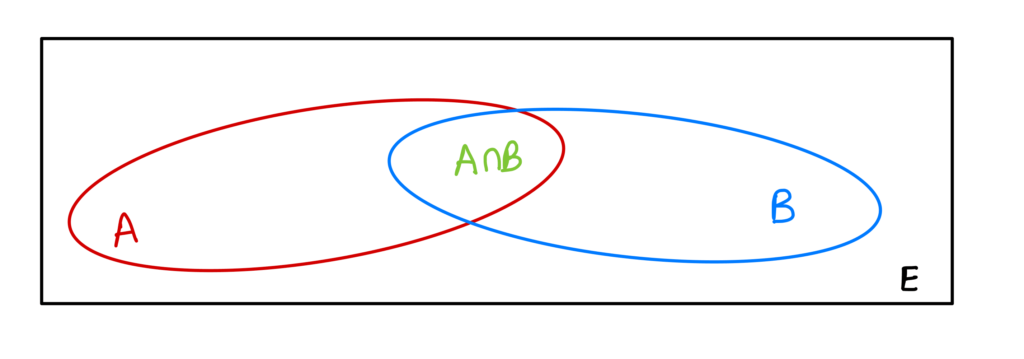
i) Si A et B sont deux ensembles finis disjoints (c’est-à-dire A \cap B=\emptyset ) alors \operatorname{card}(A \cup B)=\operatorname{card}(A)+\operatorname{card}(B).
ii) Si A_{1}, \ldots, A_{\mathrm{n}} sont des ensembles finis deux à deux disjoints alors card \left(\bigcup_{i=1}^{n} A_{i}\right)=\sum_{i=1}^{n} \operatorname{card}\left(A_{i}\right)

Proposition 4 :
Soient \mathrm{E} et F deux ensembles finis et f une application de E vers F.
i) Si f est injective alors card(E) \leqslant \operatorname{card}(F)
ii) Si f est surjective alors card(E) \geqslant \operatorname{card}(F)

Démonstration :

Proposition 5 :
Soient \mathrm{E} et F deux ensembles finis de même cardinal et f une application de \mathrm{E} vers \mathrm{F}. Les trois propositions suivantes sont équivalentes :
i) f est injective
ii) f est surjective
iii) f est bijective

Démonstration :

Proposition 6 :
Soient A et B deux ensembles finis. On a :
i) \operatorname{Card}(A \cup B)=\operatorname{card}(A)+\operatorname{card}(B)-\operatorname{card}(A \cap B).
ii) \operatorname{card}(B \backslash A)=\operatorname{card}(A \cup B)-\operatorname{card}(A)=\operatorname{card}(B)-\operatorname{card}(A \cap B)
iii) Si E est un ensemble fini contenant A alors \operatorname{card}\left(C_{E}^{A}\right)=\operatorname{card}(E)-\operatorname{card}(A)

Démonstration :

Proposition 7 :
Soient E et F deux ensembles finis. \operatorname{card}(E \times F)=\operatorname{card}(E) \times \operatorname{card}(F)

Démonstration :

Proposition 8 :
Soient E et F deux ensembles finis de cardinaux respectifs n \in \mathbb{N}^{*} et p \in \mathbb{N}^{*}.
\operatorname{card}\left(F^{E}\right)=p^{n}=\operatorname{card}(F)^{\operatorname{card}(E)}

Démonstration :

Proposition 9 :
Si E est un ensemble fini alors \mathcal{P}(E) est fini et \operatorname{card}(\mathcal{P}(E))=2^{\operatorname{card}(E)}

Démonstration :

II) Listes et combinaisons

Programme officiel dénombrement partie 2 MPSI-MP2I

Définition 1 :
Soient n \in \mathbb{N}^{*}, E un ensemble à \mathrm{n} éléments et p \in \llbracket 1, n \rrbracket.
On appelle p-arrangement d’éléments de E tout p-uplet (p-liste) d’éléments deux à deux distincts de E.
On note A_{p}(E) l’ensemble des p-arrangenents de E.

Exemple 1 :
On pose E=\{a ; b ; c\}
i) Les 1-arrangements d’éléments de E sont : a; b ; c
ii) Les 2-arrangement d’éléments de E sont : (a, b) ;(a, c) ;(b, a) ;(b, c) ;(c, a) ;(c, b)
iii) Les 3-arrangement d’éléments de E sont : (a, b, c) ;(a, c, b) ;(b, a, c) ;(b, c, a)(c, a, b) ;(c, b, a).

Définition 2 :
Soit (n, p) \in \mathbb{N} \times \mathbb{Z}. On note A_{n}^{p}=\left\{\begin{array}{l}\frac{n !}{(n-p) !} \quad \text { si } p \in \llbracket 0, n \rrbracket \\ 0 \text { sinon }\end{array}\right.

Proposition 10 :
Soient n \in \mathbb{N}^{*}, E un ensemble à \mathrm{n} éléments et p \in \llbracket 1, n \rrbracket.
\operatorname{card}\left(A_{p}(E)\right)=n(n-1) \times \cdots \times(n-p+1)=\frac{n !}{(n-p) !}=A_{n}^{p}

Démonstration :

Remarque 2 :
Soient n \in \mathbb{N}^{*} et p \in \llbracket 1, n \rrbracket. A_{n}^{p} représente aussi le nombre d’applications injectives d’un ensemble à \mathrm{p} éléments dans un ensemble à n-éléments.

Définition 3 :
Soient n \in \mathbb{N}, E un ensemble à \mathrm{n} éléments et k \in \llbracket 0, n \rrbracket.
On appelle combinaison de k-éléments de E toute partie de E à k-éléments.
On note P_{k}(E) l’ensemble des combinaisons de p-éléments de E.
P_{k}(E)=\{A \in \mathcal{P}(E) / \operatorname{card}(A)=k\}

Exemple 2 :
On pose E=\{a ; b ; c\}
i) Il y a une seule combinaison de 0-élément de E: \emptyset
ii) Les combinaisons de 1-éléments de E sont : \{a\} ;\{b\} ;\{c\}.
iii) Les combinaisons de 2 -éléments de E sont : \{a ; b\} ;\{a ; c\},\{b ; c\}
iv) Il y a une seule combinaison de 3-elément de E:\{a ; b ; c\}

Proposition 11 :
Soient \mathrm{n} un entier naturel, \mathrm{E} un ensemble à \mathrm{n} éléments et k \in \llbracket 0, n \rrbracket .
\operatorname{card}\left(\mathcal{P}_{k}(E)\right)=\left(\begin{array}{l}n \\ k\end{array}\right)

Démonstration :

III) Quelques applications du dénombrement

Cardinal de l’ensemble des parties d’un ensemble fini :
Soit \mathrm{E} un ensemble de cardinal n \in \mathbb{N}.
\mathcal{P}(E)=\bigcup_{k=0}^{n} \mathcal{P}_{k}(E)
\operatorname{Donc} \operatorname{card}(\mathcal{P}(E))=\sum_{k=0}^{n} \operatorname{card}\left(\mathcal{P}_{k}(E)\right)=\sum_{k=0}^{n}\left(\begin{array}{l}n \\ k\end{array}\right)=2^{n}

Formule de symétrie :
\forall n \in \mathbb{N}, \forall k \in \llbracket 0, n \rrbracket, \quad \binom{n}{k} = \binom{n}{n-k}

Démonstration :

Formule de Pascal :

\forall n \in \mathbb{N}, \forall k \in \llbracket 0, n \rrbracket, \quad \binom{n+1}{k+1} = \binom{n}{k} + \binom{n}{k+1}

Démonstration :

Formule du binôme :
\forall n \in \mathbb{N}, \forall(a, b) \in \mathbb{C}^{2},(a+b)^{n}=\sum_{k=0}^{n}\binom{n}{k} a^{k} b^{n-k}

Démonstration :