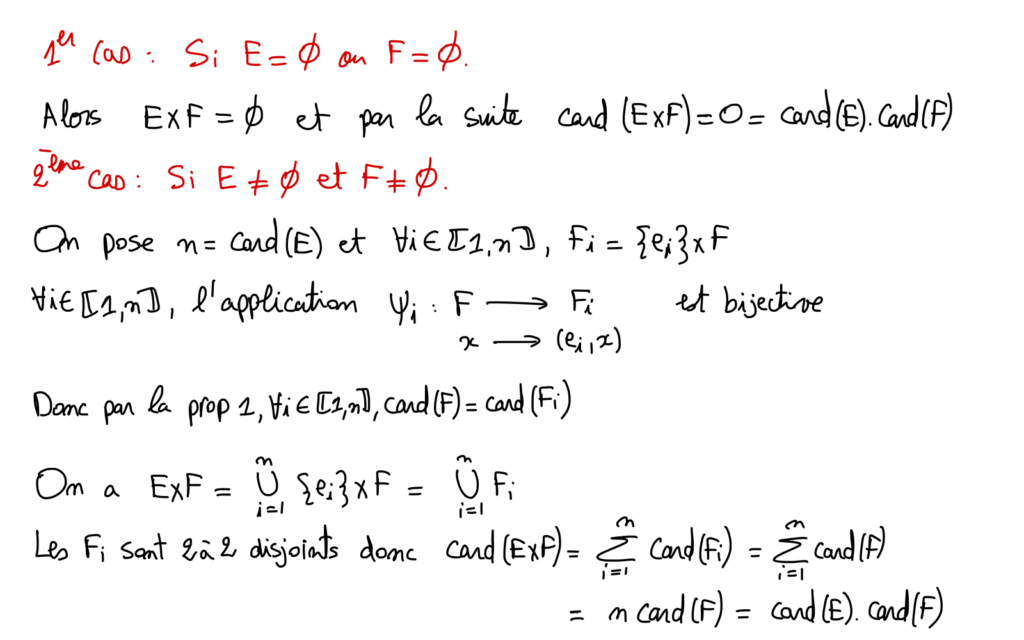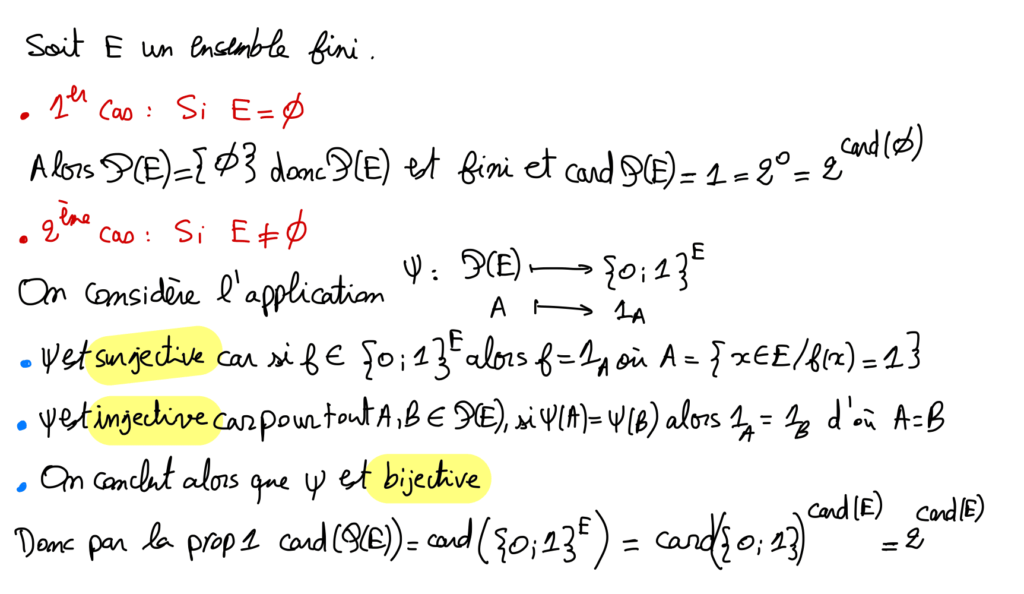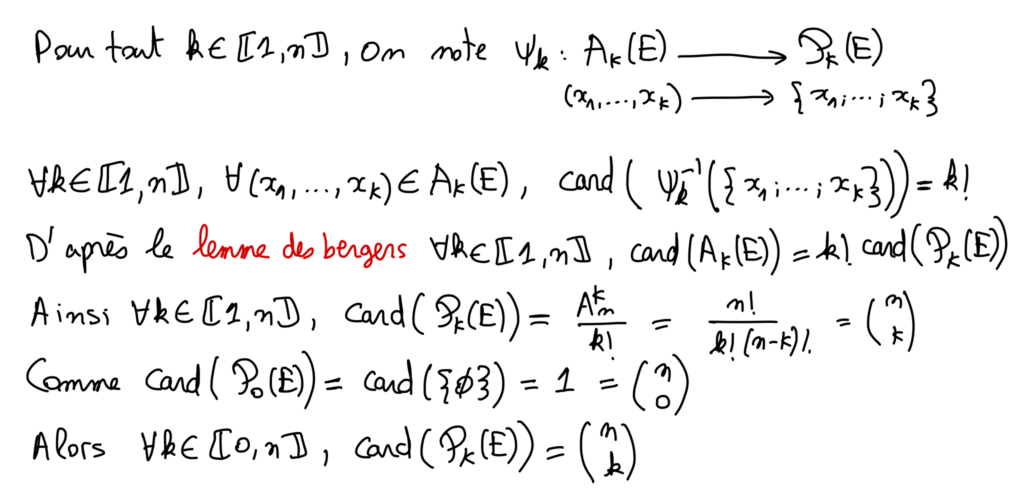Ce cours sur le dénombrement s’adresse aux étudiants des filières MPSI et MP2I. Il est introduit au programme essentiellement en vue de son utilisation en probabilités. Je vous encourage également à consulter notre série d’exercices corrigés sur le dénombrement afin d’assimiler pleinement le contenu du cours.
I) Cardinal d’un ensemble fini

Proposition-définition 1 : Soit E un ensemble.
On dit que E est un ensemble fini lorsqu’il est vide ou lorsqu’il existe un entier naturel non nul n de façon que E soit en bijection avec \llbracket 1, n \rrbracket .
Dans ce cas, n est unique, on l’appelle cardinal de E et on le note card(E) ou |E|.
On convient que card(\emptyset)=0.
Lorsque E n’est pas fini, on dit que E est infini.
Proposition 2 :
Soit E un ensemble fini.
i) Toute partie F de E est finie et de plus \operatorname{card}(F) \leqslant \operatorname{card}(E).
ii) \forall F \in \mathcal{P}(E), \operatorname{card}(E)=\operatorname{card}(F) \Leftrightarrow E=F.
Remarque 1 :
Soient E un ensemble fini et F un ensemble.
Pour montrer que F=E il suffit de montrer que F \subset E et \operatorname{card}(F)=\operatorname{card}(E).
Proposition 3 :
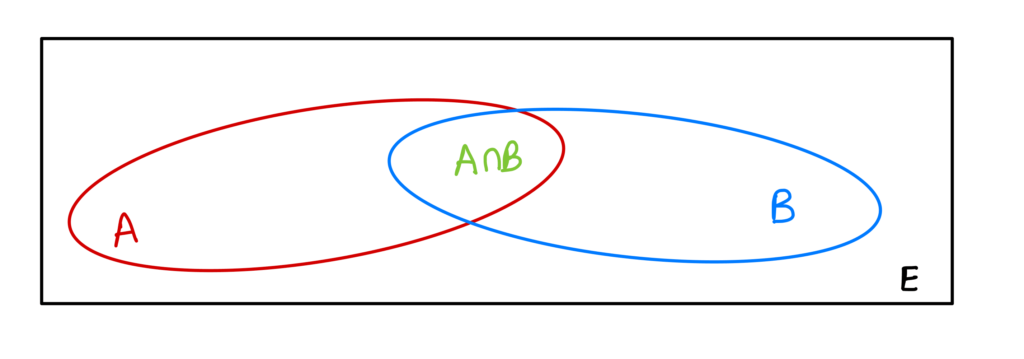
i) Si A et B sont deux ensembles finis disjoints (c’est-à-dire A \cap B=\emptyset ) alors \operatorname{card}(A \cup B)=\operatorname{card}(A)+\operatorname{card}(B).
ii) Si A_{1}, \ldots, A_{\mathrm{n}} sont des ensembles finis deux à deux disjoints alors card \left(\bigcup_{i=1}^{n} A_{i}\right)=\sum_{i=1}^{n} \operatorname{card}\left(A_{i}\right)
II) Listes et combinaisons

Définition 1 :
Soient n \in \mathbb{N}^{*}, E un ensemble à \mathrm{n} éléments et p \in \llbracket 1, n \rrbracket.
On appelle p-arrangement d’éléments de E tout p-uplet (p-liste) d’éléments deux à deux distincts de E.
On note A_{p}(E) l’ensemble des p-arrangenents de E.
Exemple 1 :
On pose E=\{a ; b ; c\}
i) Les 1-arrangements d’éléments de E sont : a; b ; c
ii) Les 2-arrangement d’éléments de E sont : (a, b) ;(a, c) ;(b, a) ;(b, c) ;(c, a) ;(c, b)
iii) Les 3-arrangement d’éléments de E sont : (a, b, c) ;(a, c, b) ;(b, a, c) ;(b, c, a)(c, a, b) ;(c, b, a).
Définition 2 :
Soit (n, p) \in \mathbb{N} \times \mathbb{Z}. On note A_{n}^{p}=\left\{\begin{array}{l}\frac{n !}{(n-p) !} \quad \text { si } p \in \llbracket 0, n \rrbracket \\ 0 \text { sinon }\end{array}\right.
Remarque 2 :
Soient n \in \mathbb{N}^{*} et p \in \llbracket 1, n \rrbracket. A_{n}^{p} représente aussi le nombre d’applications injectives d’un ensemble à \mathrm{p} éléments dans un ensemble à n-éléments.
Définition 3 :
Soient n \in \mathbb{N}, E un ensemble à \mathrm{n} éléments et k \in \llbracket 0, n \rrbracket.
On appelle combinaison de k-éléments de E toute partie de E à k-éléments.
On note P_{k}(E) l’ensemble des combinaisons de p-éléments de E.
P_{k}(E)=\{A \in \mathcal{P}(E) / \operatorname{card}(A)=k\}
Exemple 2 :
On pose E=\{a ; b ; c\}
i) Il y a une seule combinaison de 0-élément de E: \emptyset
ii) Les combinaisons de 1-éléments de E sont : \{a\} ;\{b\} ;\{c\}.
iii) Les combinaisons de 2 -éléments de E sont : \{a ; b\} ;\{a ; c\},\{b ; c\}
iv) Il y a une seule combinaison de 3-elément de E:\{a ; b ; c\}
III) Quelques applications du dénombrement
Cardinal de l’ensemble des parties d’un ensemble fini :
Soit \mathrm{E} un ensemble de cardinal n \in \mathbb{N}.
\mathcal{P}(E)=\bigcup_{k=0}^{n} \mathcal{P}_{k}(E)
\operatorname{Donc} \operatorname{card}(\mathcal{P}(E))=\sum_{k=0}^{n} \operatorname{card}\left(\mathcal{P}_{k}(E)\right)=\sum_{k=0}^{n}\left(\begin{array}{l}n \\ k\end{array}\right)=2^{n}