arctan

I) C’est quoi la fonction arctan ?

On appelle fonction arctangente, et on note arctan, la fonction réciproque de la restriction de la fonction tangente à l’intervalle ]-\frac{\pi}{2}, \frac{\pi}{2}[.
\left.\tan (]-\frac{\pi}{2}, \frac{\pi}{2}[)=\right] \lim\limits _{\substack{x \rightarrow-\frac{\pi}{2} \\ x>-\frac{\pi}{2}}} \tan (x), \lim\limits _{\substack{x \rightarrow \frac{\pi}{2} \\ x<\frac{\pi}{2}}} \tan (x)[=]-\infty,+\infty[.
Et par la suite, le domaine de définition de la fonction arctan est \mathbb{R}.
Affirmer que \arctan est la bijection réciproque de la fonction \tan, et notée \arctan = \tan^{-1}, est incorrect. Il est plus précis de déclarer que \arctan est la bijection réciproque de la restriction de la fonction tangente à l’intervalle ]-\frac{\pi}{2}, \frac{\pi}{2}[. Cette relation s’exprime comme suit : \arctan = (\tan_{/]-\frac{\pi}{2}, \frac{\pi}{2}[})^{-1}.

II) Dérivée de arctan

Nous allons démontrer que la fonction arctan est dérivable et que sa derivée est la fonction x \rightarrow \frac{1}{1+x^{2}}.
Pour cela nous allons utiliser le théorème de la dérivation de la fonction réciproque.
On sait que la fonction tan est dérivable sur ] -\frac{\pi}{2}, \frac{\pi}{2} [ et que sa derivée ne s’y annule pas, donc par le théorème de la dérivation de la fonction réciproque arctan est dérivable sur \mathbb{R}. cherchons maintenant une formule pour la dérivée de arctan.
Soit x un nombre réel, toujours par le théorème de la dérivée de la fonction réciproque, on a :
\begin{aligned} \arctan ^{\prime}(x) & =\frac{1}{\tan ^{\prime}(\arctan (x))} \\ & =\frac{1}{1+\tan ^{2}(\arctan (x))} \\ & =\frac{1}{1+x^{2}} \end{aligned}.
On a alors \forall x \in \mathbb{R}, \arctan ^{\prime}(x)=\frac{1}{1+x^{2}}.

III) La fonction arctan est de classe C^{\infty} sur \mathbb{R}.

Puisque tan est de classe C^{\infty} sur ] -\frac{\pi}{2}, \frac{\pi}{2} [ et que sa dérivée ne s’annule pas sur cet intervalle alors la fonction arctangente est également de classe C^{\infty} sur \mathbb{R}.

IV) Les propriétés de la fonction arc tangente

1) Ensemble d’arrivée de la fonction arctangente

Pour tout nombre réel x, la quantité arctan x appartient à l’intervalle ]-\frac{\pi}{2}, \frac{\pi}{2}[.

2) tan arctan x

Pour tout nombre réel x, on peut affirmer que tan arctan x  = x, ce qui peut également s’écrire en utilisant des parenthèses de la manière suivante : \tan(\arctan(x)) = x.

Voici quelques exemples :
\tan (\arctan 1)=1
\tan (\arctan 0)=0
\tan (\arctan 100)=100

3) arctan tan x

Contrairement à la formule donnant tan arctan x qu’on a traité ci-dessus et qui est valable pour tout nombre réel x, il faut être très attentif avant d’écrire arctan tan x=x.
Pour ne pas tomber dans cette erreur fréquente il suffit de se rappeler que arctan est la fonction (\tan_{/]-\frac{\pi}{2}, \frac{\pi}{2}[})^{-1} et non pas la fonction \tan ^{-1} qui n’existe pas d’ailleurs. Et par la suite on a \arctan \circ \tan_{/ ]-\frac{\pi}{2}, \frac{\pi}{2}[}=i d_{]-\frac{\pi}{2}, \frac{\pi}{2}}[ .
Ainsi Pour tout réel x compris strictement entre \frac{-\pi}{2} et \frac{\pi}{2} on a \arctan \tan x=x.

Voici quelques exemples :
\arctan \left(\tan \left(\frac{\pi}{3}\right)\right)=\frac{\pi}{3}
\arctan (\tan (\pi))=\arctan (\tan (0))=0
\arctan \left(\tan \left(\frac{9 \pi}{4}\right)\right)=\arctan \left(\tan \left(\frac{\pi}{2}+2 \pi\right)\right)=\arctan \left(\tan \left(\frac{\pi}{2}\right)\right)=\frac{\pi}{2}

4) Monotonie de la fonction arctangente

Pour étudier les variations de arctan sur \mathbb{R} on peut suivre deux méthode :
La première méthode consiste à utiliser le théorème de la bijection. En effet, comme on vient de le dire au début de cet article la fonction tan est continue et strictement croissante sur ]-\frac{\pi}{2}, \frac{\pi}{2}[. Donc le théorème de la bijection affirme que arctan a le même sens de variations que tan, c’est-à-dire strictement croissante sur \mathbb{R}.
La deuxième méthode quand-à-elle consiste à étudier le signe de arctan dérivée.
Puisqu’on a \forall x \in \mathbb{R}, \arctan ^{\prime}(x)>0, on conclut que la fonction arc tangente est strictement croissante sur \mathbb{R}.

5) arctan est impaire

Montrons que la fonction arctangente est impaire
Tout d’abord le domaine de définition de arctan est symétrique par rapport à 0.
Ensuite, fixons un nombre réel x.
On a \tan ( arctan (-x))=-x=-\tan (\arctan (x))=\tan (-\arctan (x)).
Donc \tan (\arctan (-x))=\tan (-\arctan (x)).
Donc \arctan (\tan (\arctan (-x)))=\arctan (\tan (-\arctan (x))).
Puisque \arctan (-x) et -\arctan (x) appartiennent à ]-\frac{\pi}{2}, \frac{\pi}{2}[.
On trouve \arctan (-x)=-\arctan (x).
Ceci explique bien pourquoi la fonction arc tangente est impaire.

V) Valeurs remarquable de la fonction arctangente

1) C’est combien arctan 0 ?

On peut répondre à cette question par deux manières différente :
On peut trouver la valeur de \arctan 0 en remarquant que \tan 0=0 puis on compose les deux membres de cette égalité par \arctan. On obtient alors \arctan \tan 0=\arctan 0.
Comme \arctan \tan 0=0.
On conclut que arctan 0 est égale à 0.
La deuxième méthode pour obtenir la valeur de arctan 0 est d’utiliser un argument de parité.
En effet, la fonction arc tangente est impaire et comme la courbe représentative de toute fonction impaire passe par l’origine on retrouve le fait que arctan 0 est égale à 0.

2) C’est combien \arctan 1 ?

Pour trouver la valeur de \arctan 1, remarquons d’abord que \sin \left(\frac{\pi}{4}\right)=\cos \left(\frac{\pi}{4}\right)=1 et par la suite \tan \left(\frac{\pi}{4}\right)=1.
En composant ensuite par arctan, on trouve que \operatorname{artan} 1 est égale à \frac{\pi}{4}.

3) Autres valeurs remarquables

\arctan \left(\frac{\sqrt{3}}{3}\right)=\frac{\pi}{6} car \tan \left(\frac{\pi}{6}\right)=\frac{\sin \left(\frac{\pi}{6}\right)}{\cos \left(\frac{\pi}{6}\right)}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{\sqrt{3}}{3} .
 \arctan (\sqrt{3})=\frac{\pi}{3}  car  \tan \left(\frac{\pi}{3}\right)=\frac{\sin \left(\frac{\pi}{3}\right)}{\cos \left(\frac{\pi}{3}\right)}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3} .

VI) Limites de arctan

1) Limite de x \rightarrow \frac{ \arctan x}{x} en 0

On peut calculer la limite en 0 de \arctan (x) / x en utilisant le changement de variable x=\tan (y). On a ainsi :
\begin{aligned} \lim _{x \rightarrow 0} \frac{\arctan (x)}{x} & =\lim _{y \rightarrow 0} \frac{\arctan (\tan (y))}{\tan (y)} \\& =\lim _{y \rightarrow 0} \frac{y}{\tan (y)} \\& =1\end{aligned}

2) Limites de arctan en l’infini

Toujours via le changement de variable x=\tan (y) on trouve :
\begin{aligned}\lim _{x \rightarrow+\infty} \arctan (x) & =\lim _{y \rightarrow \frac{\pi^{-}}{2}} \arctan (\tan (y)) \\& =\lim _{y \rightarrow \frac{\pi^{-}}{2}} y \\& =\frac{\pi}{2}\end{aligned}.
Pour la limite de arctan en moins l’infini il suffit d’utiliser le fait que artangente est impaire.
Ainsi :
\begin{aligned}\lim _{x \rightarrow-\infty} \arctan (x) & =\lim _{x \rightarrow+\infty} \arctan (-x) \\& =\lim _{x \rightarrow+\infty}-\arctan (x) \\& =\frac{-\pi}{2}\end{aligned}.

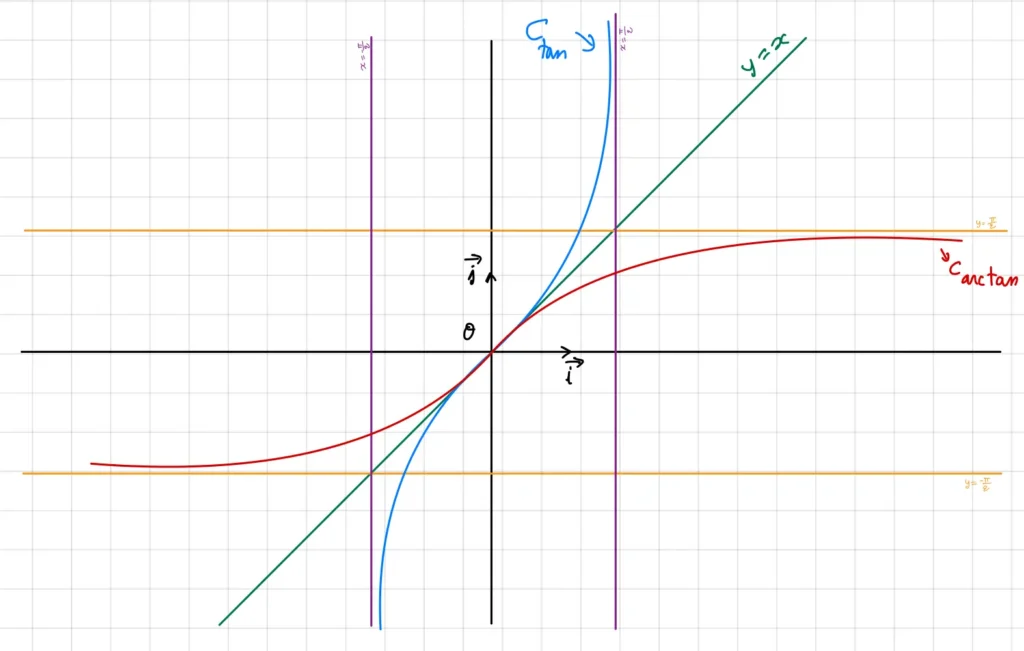
VII) Comment tracer la courbe représentative de la fonction arctan

Il y a deux méthode pour tracer la courbe de la fonction arctan dans un repère orthonormé directe (O, \vec{\imath}, \vec{\jmath}).
La première méthode consiste à utiliser le lien entre la courbe d’une fonction bijective et sa réciproque. On trace alors la courbe de la restriction de la fonction tan à ] \frac{-\pi}{2}, \frac{\pi}{2} [ puis on déduit celle de arctan par symétrie par rapport à la première bissectrice (la droite d’équation =x ).
La deuxième méthode consiste à exploiter tous les résultats qu’on vient de voir à propos de la fonction arctangente et les complétés par une étude des branches infinies.
Comme arctan est impaire il suffit de tracer sa courbe sur \mathbb{R}^{+}et la compléter sur \mathbb{R}^{-}par la symétrie de centre l’origine du repère.
Puisque \lim\limits _{x \rightarrow+\infty} \arctan (x)=\frac{\pi}{2}, la courbe représentative de la fonction arctan admet la droite d’équation y=\frac{\pi}{2} comme asymptote au voisinage de +\infty.