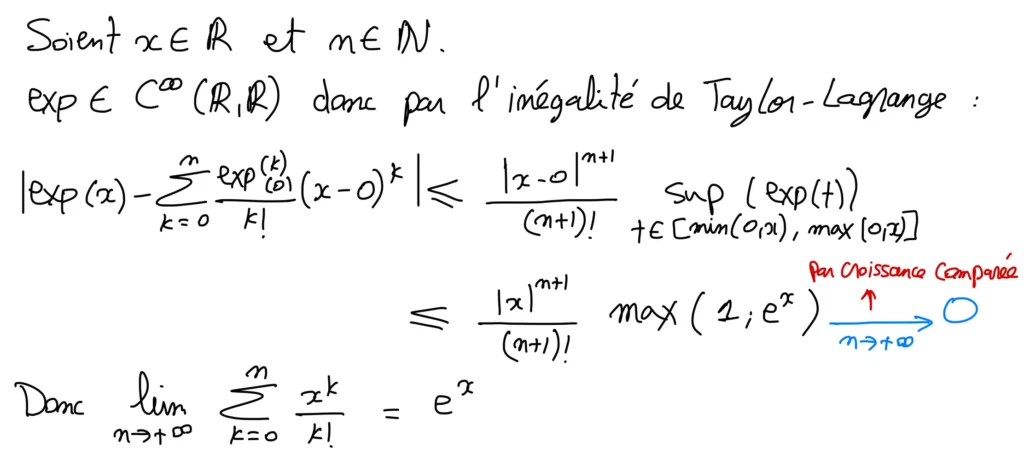Ce cours sur l’intégration est conforme au programme des filières MPSI et MP2I. Il contient des exemples et des exercices d’application qui faciliteront votre assimilation du contenu. N’hésitez pas à consulter notre série d’exercices corrigés pour acquérir une maîtrise solide de cours.


Dans tout ce cours \mathbb{K} désigne \mathbb{R} ou \mathbb{C} , a, b deux réels tels que a<b.
I) Continuité uniforme
Définition 1 :
Soient I un intervalle de \mathbb{R} et f \ : \ I \rightarrow \mathbb{K} une fonction.
On dit que f est uniformément continue sur I lorsque :
\forall \varepsilon \gt 0, \ \exists \eta \gt 0, \ \forall x,y \in I, \ (|x-y| \leq \eta \Rightarrow |f(x)-f(y)| \leq \varepsilon )
Remarque 1 :
i) Toute fonction lipschitzienne sur I est uniformément continue sur I .
ii) Toute fonction uniformément continue sur I est continue sur I .
iii) Les réciproques de i) et ii) sont fausses.
Théorème de Heine :
Toute fonction continue sur un segment y est uniformément continue.
II) Fonctions continues par morceaux
1) Subdivision d’un segment de \mathbb{R}
Définition 1 (Subdivision) :
On appelle subdivision du segment [a, b] toute famille finie de nombres réels \sigma=\left(x_{k}\right)_{0 \leq k \leq n} tels que : a=x_{0}<x_{1}<\cdots<x_{n-1}<x_{n}=b.
Le pas de la subdivision \sigma est le réel : \delta(\sigma)=\max _{i \in \llbracket 0, n-1 \rrbracket}\left(x_{i+1}-x_{i}\right).
La subdivision est dite régulière lorsque pour tout i \in \llbracket 0, n-1 \rrbracket , \ \ x_{i+1}-x_{i}=\delta(\sigma).
Le support de le subdivision \sigma est l’ensemble \left\{x_{i} / i \in \llbracket 0, n-1 \rrbracket\right\}, on le note \operatorname{Supp}(\sigma).
Si \sigma^{\prime} est une autre subdivision de [a, b], on note \sigma \cup \sigma^{\prime} la subdivision de [a, b] dont le support est \operatorname{Supp}(\sigma) \cup \operatorname{Supp}\left(\sigma^{\prime}\right).
Exemple 1 :
i) On pose x_{0}=0, \ x_{1}=2,\ x_{2}=4, \ x_{3}=6,\ x_{4}=8, \ x_{5}=10 .
\sigma=\left(x_{k}\right)_{0 \leq k \leq 5} est une subdivision régulière de [0,10] de pas \delta(\sigma)=2 et de support \operatorname{Supp}(\sigma)=\{0 ; 2 ; 4 ; 6 ; 8 ; 10\}
ii) On pose y_{0}=0, \ y_{1}=3,\ y_{2}=10. \sigma^{\prime}=\left(y_{k}\right)_{0 \leq k \leq 5} est une subdivision non régulière de [0,10] de pas \delta\left(\sigma^{\prime}\right)=7 et de support \operatorname{Supp}\left(\sigma^{\prime}\right)=\{0 ; 3 ; 10\}.
iii) On pose z_{0}=0,\ z_{1}=2, \ z_{2}=3,\ z_{3}=4, \ z_{4}=6,\ z_{5}=8, \ z_{6}=10. On a \sigma \cup \sigma^{\prime}=\left(z_{k}\right)_{0 \leq k \leq 6}.
iv) On pose pour tout k \in \llbracket 0, n \rrbracket, a_{k}=a+k \frac{b-a}{n} .
\tau=\left(a_{k}\right)_{0 \leq k \leq n} est une subdivision régulière de [a, b] de pas \delta(\tau)=\frac{b-a}{n} et de support \operatorname{Supp}(\tau)=\left\{a+k \frac{b-a}{n} / k \in \llbracket 0, n \rrbracket\right\}.
Définition 2 (Subdivision plus fine qu’une autre) :
Soient \sigma et \tau deux subdivision du segment [a, b].
On dit que \tau est plus fine que \sigma lorsque \operatorname{Supp}(\sigma) \subset \operatorname{Supp}(\tau).
Exemple 2 :
i) On pose x_{0}=0, \ x_{1}=2,\ x_{2}=4,\ x_{3}=6,\ x_{4}=8, \ x_{5}=10 et y_{0}=0,\ y_{1}=4,\ y_{2}=8, \y_{3}=10.
La subdivision \sigma=\left(x_{k}\right)_{0 \leq k \leq 5} est plus fine que la subdivision \sigma^{\prime}=\left(y_{k}\right)_{0 \leq k \leq 3}.
ii) Si \sigma et \sigma^{\prime} sont deux subdivisions de [a, b] alors \sigma \cup \sigma^{\prime} est une subdivision du segment [a, b] plus fine que \sigma et que \sigma^{\prime}.
2) Fonctions en escaliers
Définition 3 (Fonction en escalier sur un segment de \mathbb{R} ) :
Soit \varphi \in \mathcal{F}([a, b], \mathbb{K}), on dit que \varphi est une fonction en escalier sur le segment [a, b] lorsqu’il existe une subdivision \sigma=\left(x_{k}\right)_{0 \leq k \leq n} de [a, b] telle que \varphi est constante sur chaque intervalle ] x_{k}, x_{k+1}[.
C’est-à-dire : \left.\forall k \in \llbracket 0, n-1 \rrbracket, \exists c_{k} \in \mathbb{K}, \forall x \in\right] x_{k}, x_{k+1}\left[, \varphi(x)=c_{k}\right.
On dit dans ce cas que la subdivision \sigma est adaptée à la fonction en escalier \varphi.
On note \mathcal{E}([a, b], \mathbb{K}) l’ensemble des fonctions en escalier sur [a, b] à valeurs dans \mathbb{K}.
Exemple 3 :
i) Si f est une fonction constante sur le segment [a, b] alors f est une fonction en escalier sur [a, b] et toute subdivision du segment [a, b] est adaptée à f.
ii) La restriction, au segment [a, b], de la fonction partie entière est une fonction en escalier sur [a, b] et la subdivision de support ([a, b] \cap \mathbb{N}) \cup\{a ; b\} est adaptée à f.
iii) La fonction f définie pour tout x \in[0,1] par f(x)= \begin{cases} -1, \ si \ x \in [0, \frac{1}{2} ] \\ 1, \ si \ x \in ]\frac{1}{2} , 1]\end{cases} est une fonction en escalier sur [0,1].
On pose x_{0}=0, \ x_{1}=\frac{1}{2}, \ x_{2}=1. La subdivision \sigma=\left(x_{k}\right)_{0 \leq k \leq 2} est adaptée à f.
Remarque 1 :
Soit f \in \mathcal{E}([a, b], \mathbb{K}) et \sigma une subdivision de [a, b] adaptée à f.
Si \tau est une subdivision de [a, b] plus fine que \sigma alors \tau est une subdivision adaptée à f.
Remarque 2 :
Une fonction en escalier sur un segment prend un nombre finie de valeurs, elle est donc bornée.
3) Fonctions continues par morceaux.
Définition 4 (Fonction continue par morceaux sur un segment de \mathbb{R} ) :
Soit f \in \mathcal{F}([a, b], \mathbb{K}), on dit que f est une fonction continue par morceaux sur le segment [a, b] lorsqu’il existe une subdivision \sigma=\left(x_{k}\right)_{0 \leq k \leq n} de [a, b] telle que \forall k \in \llbracket 0 ; n \rrbracket, f_{/] x_{k}, x_{k+1}[} est continue sur l’intervalle ]x_{k}, x_{k+1} [ et admet des limites finies à droite en x_{k} et à gauche en x_{k+1}.
On dit dans ce cas que la subdivision \sigma est adaptée à la fonction f.
On note C M([a, b], \mathbb{K}) l’ensemble des fonctions continues par morceaux sur [a, b] à valeurs dans \mathbb{K}.
Exemple 4 :
i) Toute fonction continue sur un segment y est continue par morceaux.
ii) Toute fonction en escalier sur un segment y est continue par morceaux.
iii) La fonction f définie pour tout x \in[0,1] par f(x)= \begin{cases}-2, \ si \ x=0 \\ x-1, \ si \ x \in ] 0, \frac{1}{3} ] \\ \frac{1}{x}, \ si \ x \in ] \frac{1}{3}, 1[ \\ 5, \ si \ x=1 \end{cases} est une fonction continue par morceaux sur [0,1].
On pose x_{0}=0, \ x_{1}=\frac{1}{3}, \ x_{2}=1. La subdivision \sigma=\left(x_{k}\right)_{0 \leq k \leq 2} est adaptée à f.
Remarque 3 :
Soient f \in C M([a, b], \mathbb{K}) et \sigma une subdivision de [a, b] adaptée à f.
Si \tau est une subdivision de [a, b] plus fine que \sigma alors \tau est une subdivision de [a, b] adaptée à f.
III) Intégration d’une fonction continue par morceaux sur un segment
1) Intégrale d’une fonction en escalier
Exemple 5 :
i) Si f est constante égale à c alors \int_{a}^{b} f(x) d x=c(b-a). Car la famille (a, b) est une subdivision de [a, b] adaptée à f.
ii) \forall n \in \mathbb{N}^{*}, \int_{0}^{n}\lfloor x\rfloor d x=\sum_{k=0}^{n-1} k((k+1)-k)=\frac{n(n-1)}{2}.
En effet, pour tout entier naturel non nul n, la famille (k)_{k \in \llbracket 0, n \rrbracket} est une subdivision du segment [0, n] adaptée à la fonction en escalier x \rightarrow\lfloor x\rfloor et \forall x \in] k, k+1[,\lfloor x\rfloor=k.
2) Approximation d’une fonction continue par morceaux par des fonctions en escaliers.
3) Intégrale d’une fonction continue par morceaux
4) Intégration des fonctions à valeurs dans \mathbb{C}
Les propriétés des fonctions continues par morceaux à valeurs dans \mathbb{R} (à l’exception de celle en rapport avec l’ordre) sont valables pour les fonctions continues par morceaux à valeurs dans \mathbb{C}. Et pour f \in C M([a, b], \mathbb{C}) on a :
\int_{a}^{b} f(t) d t=\int_{a}^{b} \operatorname{Re}(f)(t) d t+i \int_{a}^{b} \operatorname{Im}(f)(t) d t.
IV) Lien entre intégrale et primitive
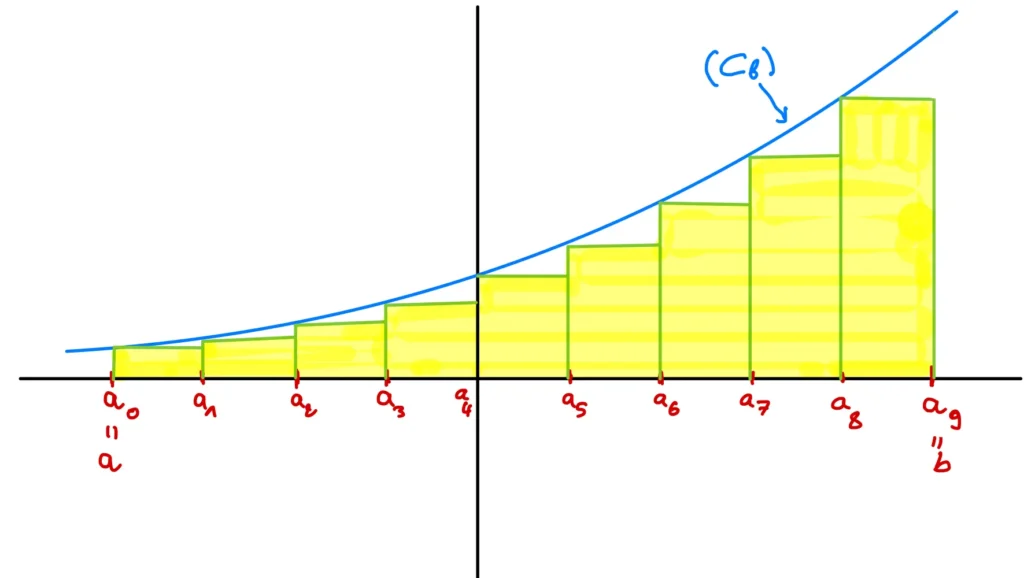
V) Sommes de Riemann
Interprétation géométrique :
VI) Formules de Taylor
Remarque 4 :
A l’aide de la formule de Taylor avec reste intégral on démontre la formule de Taylor-Young.
Exemple 7 :
i) \forall x \in \mathbb{R}, \quad e^{x}=\sum_{k=0}^{n} \frac{x^{k}}{k !}+\int_{0}^{x} \frac{\mathrm{e}^{\mathrm{t}}}{n !}(x-t)^{n} d t
ii) \forall x \in \mathbb{R}, \quad \sin (x)=x-\frac{x^{3}}{6}+\int_{0}^{x} \frac{\sin (t)}{6}(x-t)^{3} d t.