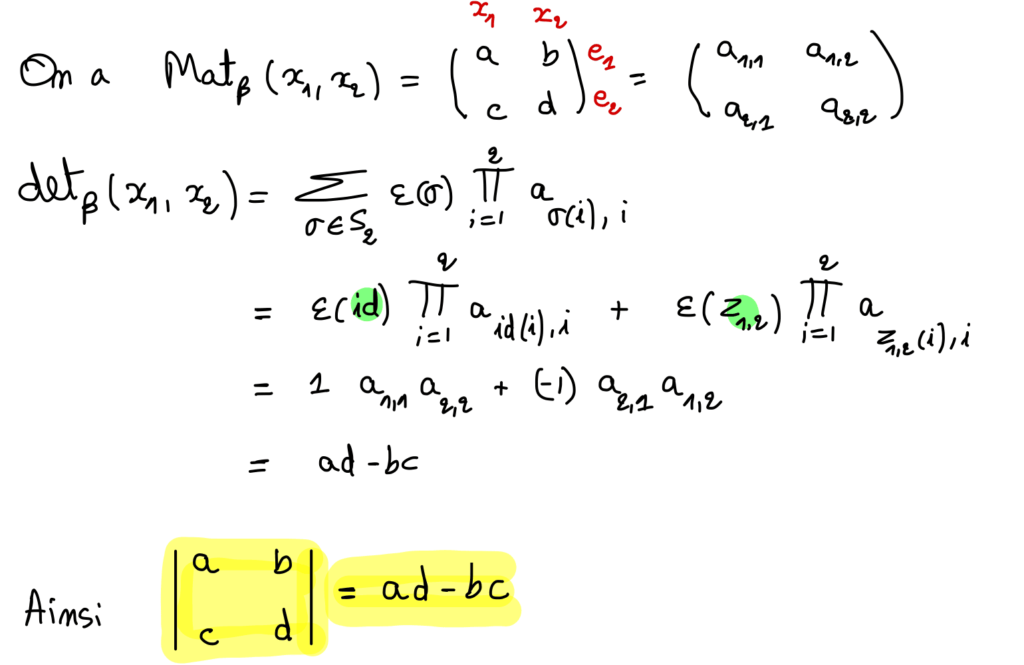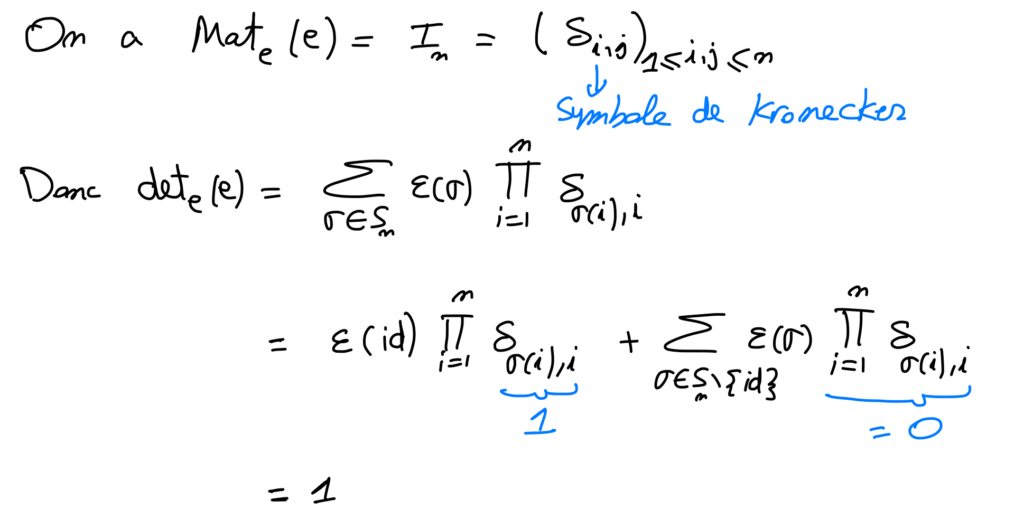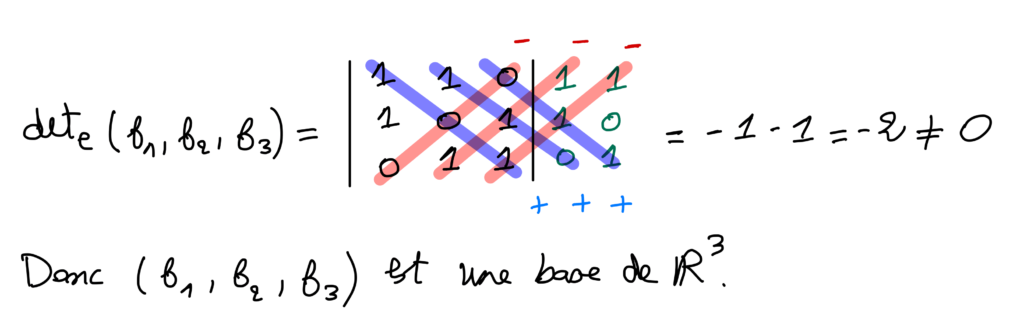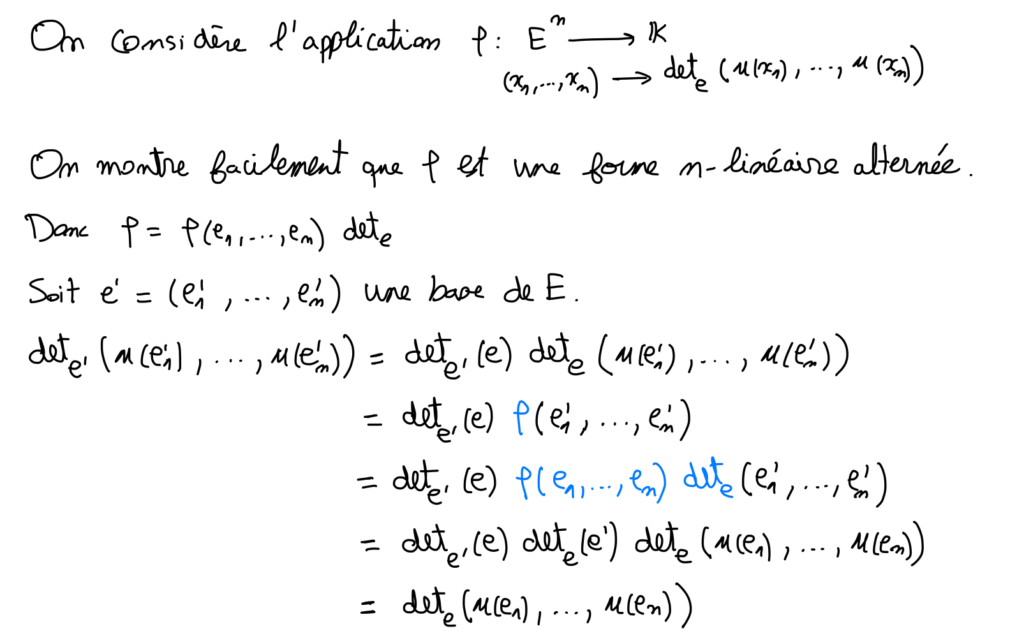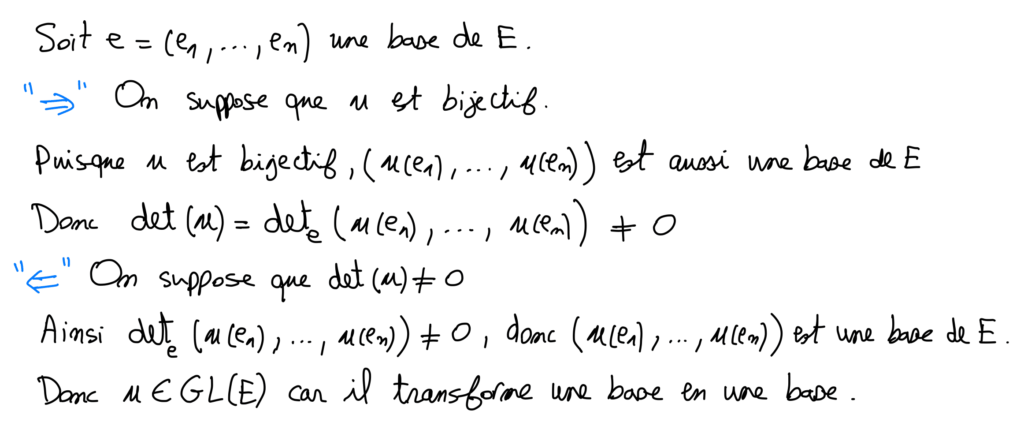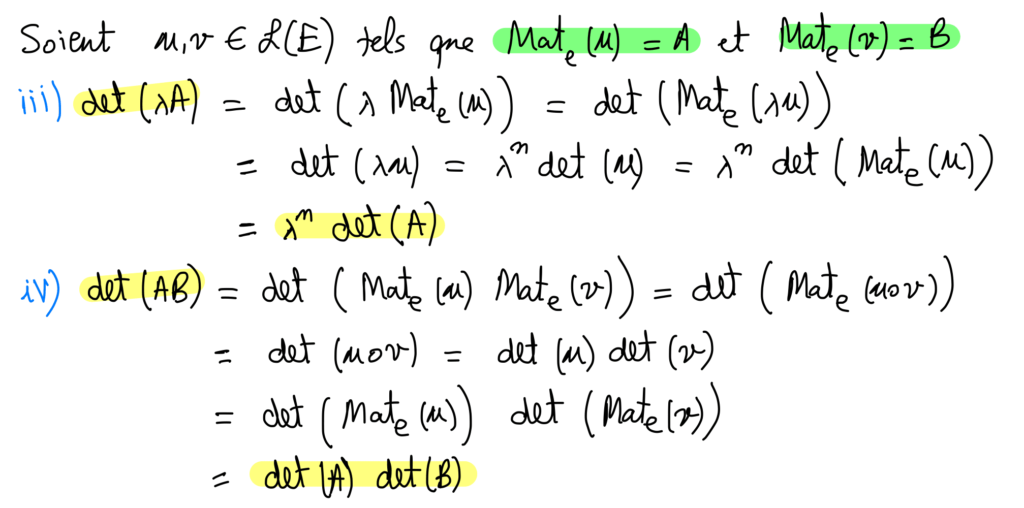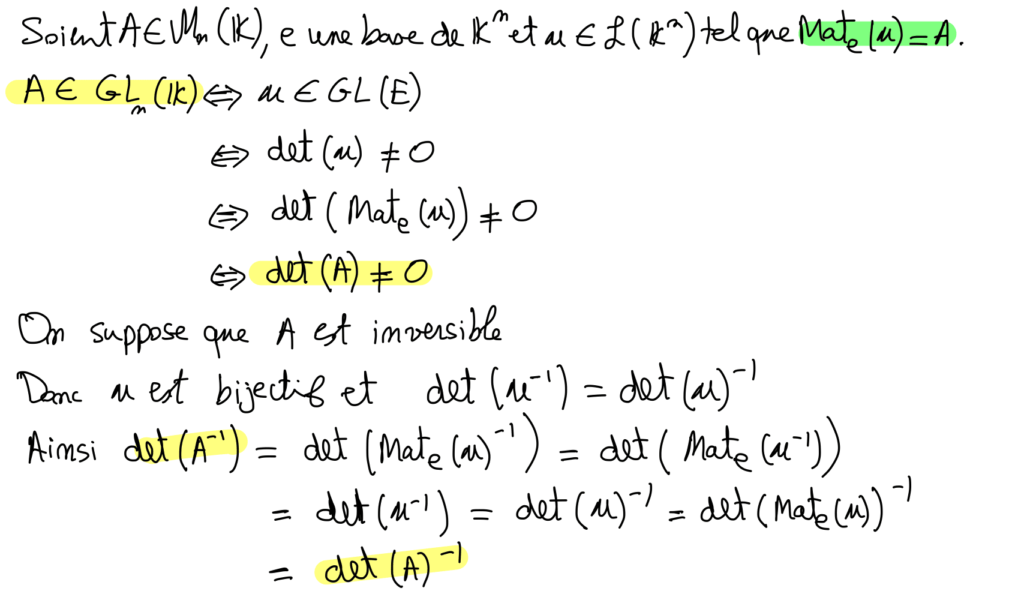Ce cours sur le déterminant s’adresse aux étudiants en prépa MPSI et MP2I. Il contient des exemples et des exercices d’application qui faciliteront votre assimilation du contenu. N’hésitez pas à consulter notre série d’exercices corrigés pour acquérir une maîtrise solide de cours.


Dans tout ce chapitre, n est un entier naturel non nul, \mathbb{K} désigne \mathbb{R} \ ou \ \mathbb{C} et E est un \mathbb{K} -espace vectoriel de dimension n.
I) Formes n-linéaires alternées
Définition d’une forme n-linéaire alternée :
Soit f \ : E^{n} \rightarrow \mathbb{K} une application. On dit que f est une forme n-linéaire sur E lorsque : \forall i \in \llbracket 1,n \rrbracket , \ \forall (x_{1},x_{2},\dots,x_{n}) \in E^{n} l’application \begin{matrix} f_{i}&:&E&\rightarrow& \mathbb{K} \\ & & x&\rightarrow & f(x_{1},x_{2},\dots,x_{i-1},x,x_{i+1},\dots,x_{n}) \end{matrix} est linéaire.
Définition d’une forme alternée :
On dit qu’une forme n-linéaire f , sur E, est alternée lorsque :
\forall (x_{1}, \dots , x_{n}) \in E^{n}, \forall (i,j) \in \llbracket 1,n \rrbracket ^{2} \ avec \ i \ne j , \ \ \ [ x_{i} = x_{j} \Rightarrow f(x_{1}, \dots , x_{n})=0 ]\ .
Exemple 2 :
L’application det définie dans l’exemple 1 est alternée.
Définition d’une forme antisymétrique :
On dit qu’une forme n-linéaire f , sur E, est antisymétrique lorsque :
\forall (x_{1}, \dots , x_{n}) \in E^{n}, \forall (i,j) \in \llbracket 1,n \rrbracket ^{2} \ avec \ i < j , \ \ \ f(x_{1}, x_{2} \dots , x_{n}) = - f(x_{1}, \dots , x_{i-1} , x_{j} , x_{i+1} ,\dots ,x_{j-1} , x_{i} , x_{j+1} , \dots , x_{n}) .
Exemple 3 :
L’application det définie dans l’exemple 1 est antisymétrique.
II) Déterminant d’une famille de vecteur dans une base
Dans toute cette partie on note \beta = (e_{1}, \dots , e_{n}) une base de E.
1) Définition et propriétés
Définition du déterminant d’une famille de vecteurs :
Soit (x_{1}, \dots , x_{n}) une famille de vecteurs de E. On pose Mat_{ \beta } (x_{1}, \dots , x_{n}) = (a_{ i,j} )_{1 \leq i,j \leq n } .
On appelle déterminant de la famille (x_{1}, \dots , x_{n}) dans la base \beta , et on note det_{ \beta } (x_{1}, \dots , x_{n}) , le scalaire suivant :
det_{ \beta } (x_{1}, \dots , x_{n}) = \sum_{\sigma \in S_{n} } \varepsilon ( \sigma ) \prod_{i=1}^{n} a_{ \sigma (i) , i } .
On le note dans ce cas : \begin{vmatrix} a_{1,1} & \dots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{n,1} & \dots & a_{n,n} \end{vmatrix} .
Règle de Sarrus :
La règle de Sarrus est une méthode de calcul utilisée uniquement pour les déterminants de taille 3, et elle est plus pratique lorsque tous les coefficients du déterminant sont des valeurs numériques connues plutôt que des paramètres variables.
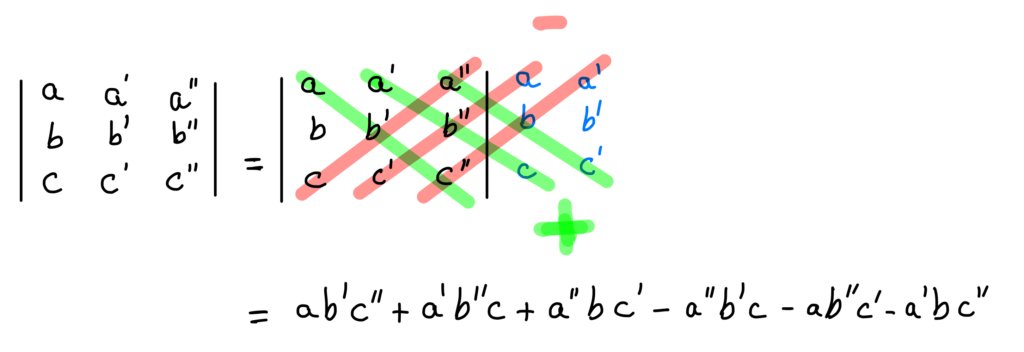
2) Orientation d’un \mathbb{R} -espace vectoriel
Dans toute cette partie E est un \mathbb{R} -espace vectoriel de dimension n \in \mathbb{N} .
Définition 1 :
i) On dit que deux bases e et e’ de E ont la même orientation lorsque e \mathcal{R} e' .
ii) Orienter E, c’est choisir arbitrairement une base de référence \beta puis appeler base directe toute base ayant la même orientation que \beta et base indirecte toute base n’ayant pas la même orientation que \beta .
Exemple 7 :
On suppose que \mathbb{R}^3 est orienté et que e=(e_{1},e_{2},e_{3} ) est une base directe de \mathbb{R}^3 .
On note e'=(-e_{1},-e_{3}, -e_{2} ) .
det_{e}(e')=(-1)^{3} det_{e} (e_{2},e_{3},e_{1} ) = (-1)^{3} (-1)^{2} det_{e} (e_{1},e_{2},e_{3} ) =-1 .
det_{e}(e') <0 , e’ est alors une base indirecte de \mathbb{R}^3 .
Remarque 1 :
i) Dans \mathbb{R}^2 muni de sa base canonique e, l’aire algébrique du parallélogramme associé à la famille de vecteurs (\vec{u} , \vec{v} ) est det_{e} (\vec{u} , \vec{v} ) .
ii) Dans \mathbb{R}^3 muni de sa base canonique e, le volume algébrique du parallélépipède associé à la famille de vecteurs (\vec{u} , \vec{v} , \vec{w} ) est det_{e} (\vec{u} , \vec{v} , \vec{w} ) .
III) Déterminant d’un endomorphisme
Remarque 2 :
D’après la démonstration, pour tout (x_1 , \dots , x_n ) \in E , \ \ det_{e} ( u(x_1) , \dots , u(x_n))=det(u) det_{e} (x_1, \dots , x_n )
Remarque 3 :
i) \forall u \in \mathcal{L} (E), \forall p \in \mathbb{N}, det(u^p)=det(u)^p .
ii) \forall u \in GL(E), \forall p \in \mathbb{Z}, det(u^p)=det(u)^p .
iii) En général, pour u,v \in \mathcal{L} (E), \ \ det(u+v) \ne det(u)+det(v) .
Par exemple, lorsque n \geq 2, \ \ det(id_E + id_E )=2^n \ne 2 = det(id_E) +det(id_E) .
iv) \forall u,v \in \mathcal{L} (E), \ det(u \circ v)=det(v \circ u) .
v) L’application \begin{matrix} \varphi & : & (GL(E), \circ )& \rightarrow & ( \mathbb{K}^* , \times ) \\ & & u & \rightarrow & det(u) \end{matrix} est un morphisme de groupe surjectif, non injectif.
En effet,
Soit \lambda \in \mathbb{K} , on définit u \in \mathcal{L} (E) \ par \ u(e_1)= \lambda e_1 \ et \ \forall i \in \llbracket 2,n \rrbracket , \ \ u(e_i)=e_i .
On a det(u)=det_{e} (u(e_1), u(e_2), \dots , u(e_n))= det_{e} (\lambda e_1, e_2, \dots , e_n)=\lambda det_{e} ( e_1, e_2, \dots , e_n) = \lambda .
Donc u est surjectif.
Pour la non injectivité il suffit de considérer l’endomorphisme de E définie par u(e_1)= 2 e_1 , \ u(e_2)= \frac{1}{2} e_2 \ et \ \forall i \in \llbracket 3,n \rrbracket , \ \ u(e_i)=e_i .
On a det(u)=det_{e} (u(e_1), u(e_2), \dots , u(e_n))= det_{e} (2 e_1, \frac{1}{2} e_2, e_3, \dots , e_n)= det_{e} ( e_1, e_2, \dots , e_n) =1=det(id) .
Et u \ne id_E donc det n’est pas injectif en général pour n \geq 2 .
IV) Déterminant d’une matrice carrée
Définition du déterminant d’une matrice :
Soit A = (a_{ i,j} )_{1 \leq i,j \leq n } \in \mathcal{M}_{n} ( \mathbb{K} ) .
On définit le déterminant de la matrice carrée A par la formule :
det(A)= \sum_{\sigma \in S_{n} } \varepsilon ( \sigma ) \prod_{i=1}^{n} a_{ \sigma (i) , i } .
On le note dans ce cas : \begin{vmatrix} a_{1,1} & \dots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{n,1} & \dots & a_{n,n} \end{vmatrix} .
Remarque 4 :
Soient e=(e_1 , \dots , e_n) une base de E, \mathcal{F} = (x_1 , \dots , x_n ) une famille de vecteurs de E et u \in \mathcal{L} (E) . On a :
i) det_{e} ( \mathcal{F} ) = det ( Mat_{e} (u) .
ii) det(u) = det_e ( u( e_1) ,\dots , u( e_n )) = det (Mat_{e} (u)) .
Remarque 5 :
i) \forall A \in \mathcal{M}_{n} ( \mathbb{K} ) , \forall k \in \mathbb{N}, det(A^k)=det(A)^k .
i) \forall A \in GL_{n} ( \mathbb{K} ) , \forall k \in \mathbb{Z}, det(A^k)=det(A)^k .
iii) En général, pour A,B \in \mathcal{M}_{n} ( \mathbb{K} ), \ \ det(A+B) \ne det(A)+det(B) .
Par exemple, lorsque n \geq 2, \ \ det(I_n + I_n )=2^n \ne 2 = det(I_n) +det(I_n) .
iv) A,B \in \mathcal{M}_{n} ( \mathbb{K} ), \ det(AB)=det(BA) .
v) L’application \begin{matrix} \varphi & : & (GL_n(\mathbb{K}), \times )& \rightarrow & ( \mathbb{K}^* , \times ) \\ & & A & \rightarrow & det(A) \end{matrix} est un morphisme de groupe surjectif, non injectif (non injectif si n \geq 2 ).
vi) Deux matrices semblables ont le même déterminant.
Remarque 6 :
Cette proposition met en évidence le caractère n-linéaire alterné du déterminant par rapport aux lignes.
IV) Calcul des déterminants
Effet des opérations élémentaires sur le déterminant :
Grace au caractère n-linéaire alterné du déterminant par rapport aux lignes et aux colonnes on obtient les résultats suivants :
i) Transvection : Ajouter à une colonne (Resp. à une ligne) une combinaison linéaire des autres colonnes (Resp. lignes) ne change pas la valeur du déterminant.
ii) Permutation : Permuter deux colonnes ou deux lignes revient à multiplier le déterminant par -1.
iii) Dilatation : Multiplier une colonne (Resp. une ligne) par un scalaire \lambda revient à multiplier le déterminant par \lambda .
Définition (mineur, cofacteur et comatrice) :
Soient A=(a_{i,j} ) \in \mathcal{M}_{n} (\mathbb{K} ) \ et \ i,j \in \llbracket 1,n \rrbracket .
i) On appelle mineur associé à (i,j) le déterminant de la matrice obtenue en éliminant le i^{ème} ligne et la j^{ème} de A. On le note \Delta_{i,j} .
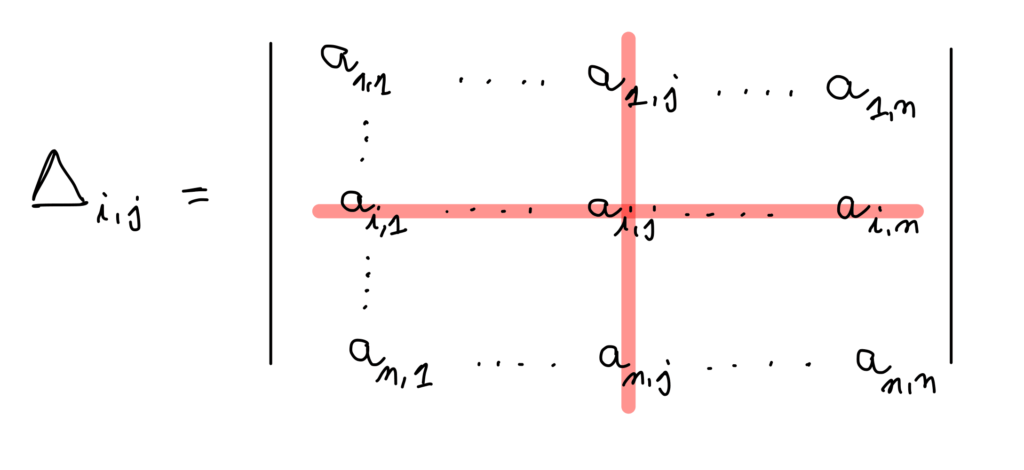
ii) On appelle cofacteur associé à (i,j) le scalaire A_{i,j} = (-1)^{i+j} \Delta_{i,j} .
iii) On appelle comatrice associée à A, et on note com(A), la matrice définie par :
com(A)= (A_{i,j} )_{1 \leq i,j \leq n } \in \mathcal{M}_{n} ( \mathbb{K} ).
Exemple 8 :
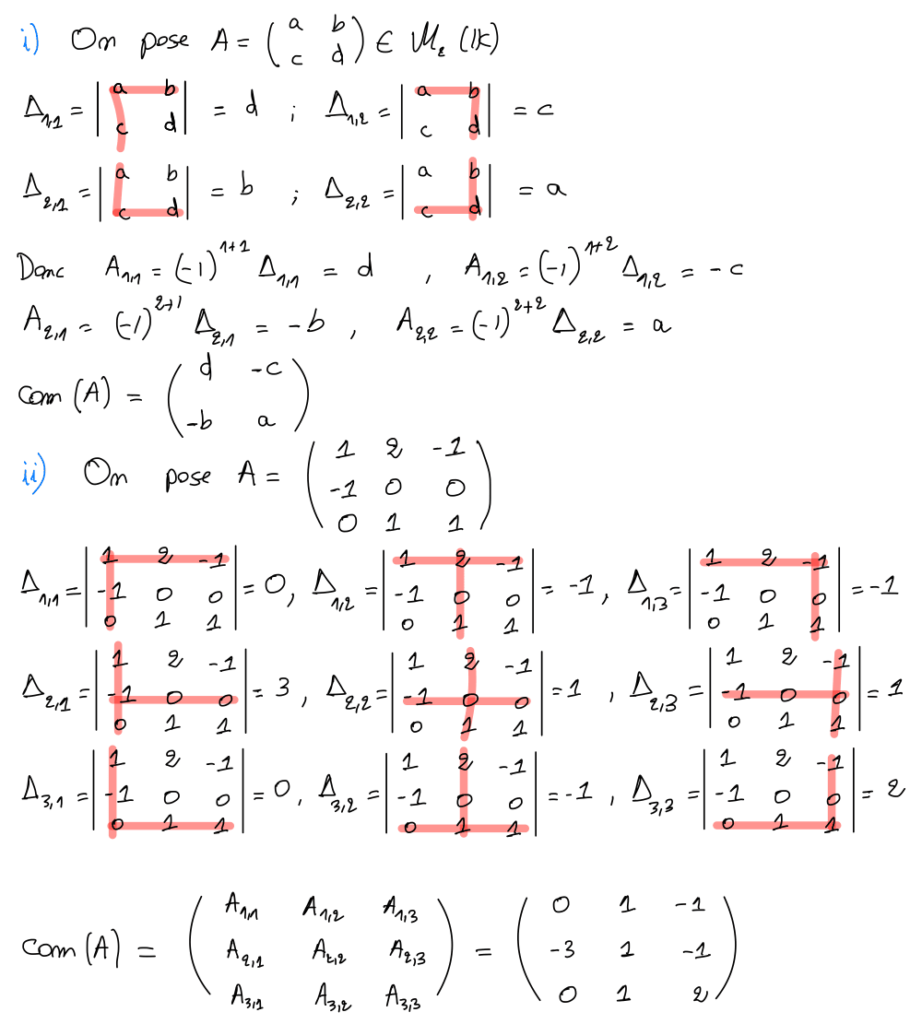
Exemple 9 :
On pose \Delta = \begin{vmatrix} a&b&c \\ x&y&z \\ e&f&g \end{vmatrix} .
i) En développant par rapport à la première colonne on trouve :
\Delta =a \begin{vmatrix} y&z \\ f&g \end{vmatrix} -x \begin{vmatrix} b&c \\ f&g \end{vmatrix} +e\begin{vmatrix} b&c \\ y&z \end{vmatrix} .
ii) En développant par rapport à la deuxième ligne on trouve :
\Delta =-x \begin{vmatrix} b&c \\ f&g \end{vmatrix} +y \begin{vmatrix} a&c \\ e&g \end{vmatrix} -z\begin{vmatrix} a&b \\ e&f \end{vmatrix} .
Exemple 10 :
On pose \Delta = \begin{vmatrix} 1&1&1&1 \\ 1&-1&1&-1 \\ 1&2&4&8 \\ 1&-2&4&-8 \end{vmatrix} .
On remarque que \Delta = V(1,-1,2,-2) .
Donc \Delta = (-2-1)(2-1)(-1-1)(-2+1)(2+1)(-2-2)=72 .